习题答案
第1章
一、1.14. 2.2. 3.0. 4.1. 5.3.
二、1.C. 2.D. 3.A. 4.B. 5.D.
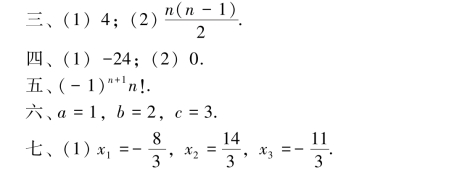
八、λ=-1或λ=4时有非零解.
九、(1)xn+(-1)n+1yn;(2)(x+(n-1)a)(x-a)n-1.
十、提示:按一行(列)展开和递归的方式计算出行列式的值.
第2章
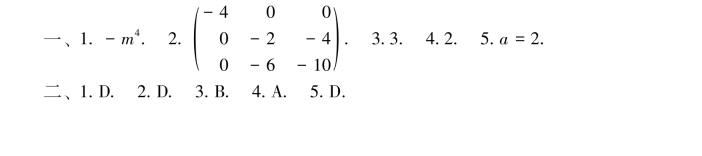

第3章

2.当λ≠-2且λ≠1时,β可由α1,α2,α3线性表示,且表达式唯一.
四、提示:1.定义法.2.反证法.3.R(A)=R(B)=R(A,B).4.只需证明两个向量组等价.
五、V1,V2都是向量空间.
六、当a=-10时,α1,α2,α3,α4线性相关;α2,α3,α4为其一个最大线性无关组(不唯一),α1=-α2-α3-α4.
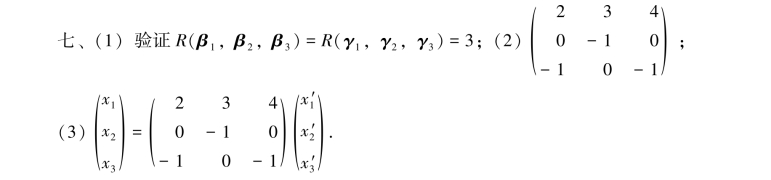
第4章

三、基础解系:
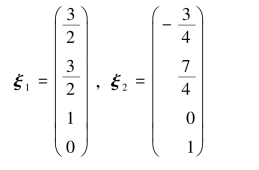
并由此得到通解:
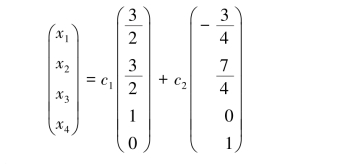 (https://www.daowen.com)
(https://www.daowen.com)
其中,c1,c2为任意实数.

八、提示:先证明α1+α2,α1+α3,α1均是解,再证明它们线性无关.
九、(1)当λ≠1且λ≠-2时,方程组有唯一解;(2)当λ=-2时,方程组无解;
(3)当λ=1时,方程组有无穷多个解,通解为
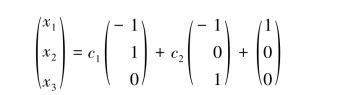
其中,c1,c2为任意实数.
![]()
十一、用定义法证明线性无关.
十二、提示:把x=k1η1+k2η2+…+ksηs代入Ax=b.
十三、提示:考虑非齐次线性方程组解的性质及齐次线性方程组解的结构.
第5章

第6章

四、(1)提示:用线性变换定义证明;(2)提示:用T的定义证明.
五、提示:先证明β1,β2,…,βn线性无关,再证明V中任一向量都可由β1,β2,…,βn线性表示.
六、提示:求出线性变换后的矩阵,由已知条件证明其行列式不等于零,故对应行向量组也线性无关.
七、(1)用子空间定义验证;(2)C(A)=Rn×n;(3)Eii(i=1,2,…,n)(主对角线上第i个元素为1,其余元素均为0的n阶方阵)是C(A)的一个基,维数为n.
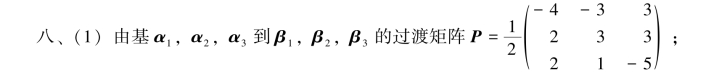
(2)T在基α1,α2,α3下的矩阵也为(1)中的P;
(3)T在基β1,β2,β3下的矩阵也为(1)中的P.
