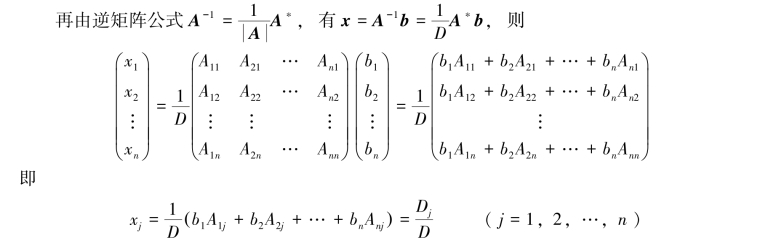2.4.2 分块矩阵的运算
分块矩阵的运算规则与普通矩阵的运算规则相类似,分别说明如下.1)分块矩阵的加法
设矩阵A=(aij)m×n,B=(bij)m×n,采用同样的分块方法,有
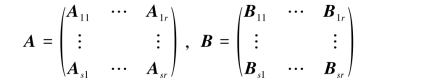
其中,Aij与Bij的行数与列数都相同,则
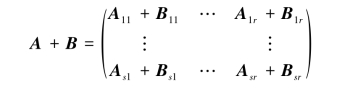
2)数乘分块矩阵

3)分块矩阵的乘法

其中,Ai1,Ai2,…,Ait(i=1,2,…,s)的列数分别等于B1j,B2j,…,Btj(j=1,2,…,r)的行数,则
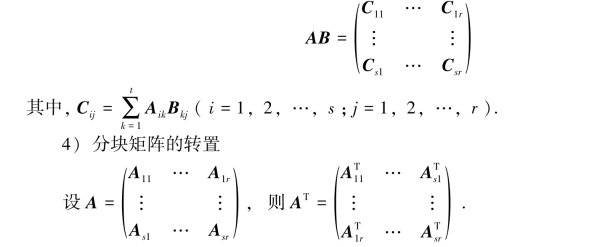
5)分块对角阵
在n阶方阵A的分块矩阵中,若只有在主对角线上有非零子块,而其余子块均为零矩阵,且在对角线上的子块都是方阵,即
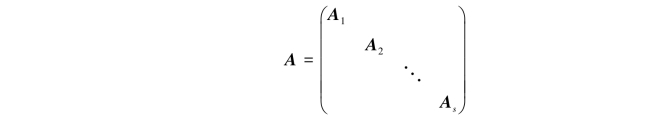
其中,Ai(i=1,2,…,s)都是方阵,则称A为分块对角阵.

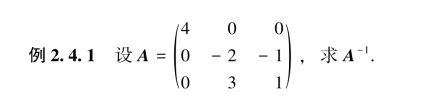
解 对矩阵A进行如下分块:
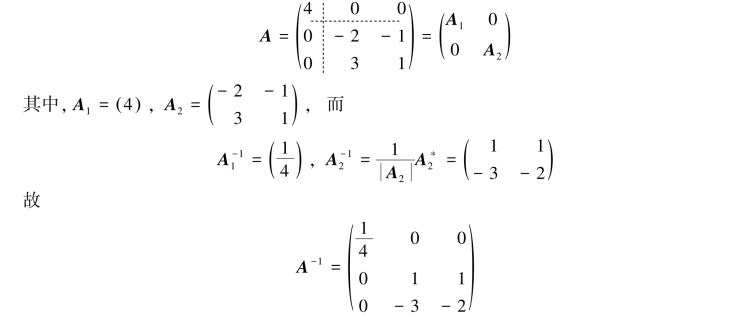
对矩阵分块时,有两种分块法应予特别重视,这就是按行分块和按列分块.
m×n矩阵A有m行,称为矩阵A的m个行向量.若第i行记作
![]()
则矩阵A可记作
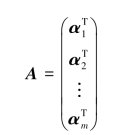
m×n矩阵A有n列,称为矩阵A的n个列向量.若第j列记作
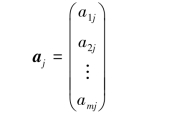
则矩阵A可记作
![]()
对于矩阵A=(aij)m×s与B=(bij)s×n的乘积矩阵AB=C=(cij)m×n,若把A按行分成m块,把B按列分成n块,则有
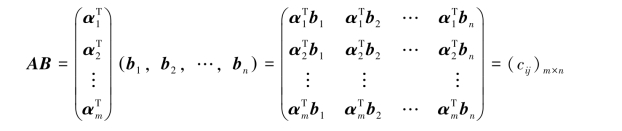
其中

由此可进一步领会矩阵相乘的定义.
以对角阵Λm左乘矩阵Am×n时,把A按行分块,有(https://www.daowen.com)

可见以对角阵Λm左乘A的结果是A的每一行都乘以Λ中与该行对应的对角元.
以对角阵Λn右乘矩阵Am×n时,把A按列分块,有
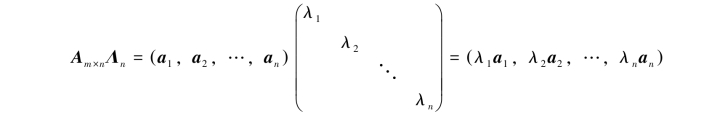
可见以对角阵Λn右乘A的结果是A的每一列都乘以Λ中与该列对应的对角元.
例2.4.2 证明矩阵A=O的充分必要条件是方阵ATA=O.
证明 条件的必要性是显然的,下面证明条件的充分性.

即A=O.
例2.4.2阐明了矩阵A与方阵ATA之间的一种关系.特别地,当A=a为列向量时,由于aTa为1×1矩阵,即aTa是一个数,这时,例2.4.2的结论可叙述为:列向量a=0的充分必要条件是aTa=0.
对于线性方程组(2.3):
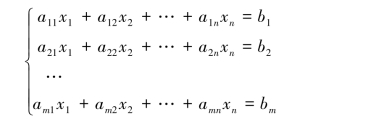
记
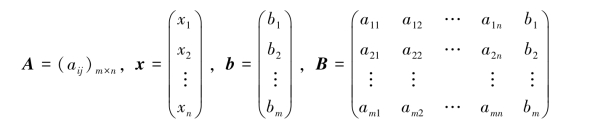
其中,A称为系数矩阵;x称为未知数向量;b称为常数项向量;B称为增广矩阵.按分块矩阵的记法,可记作
![]()
利用矩阵的乘法,方程组(2.3)可以写成矩阵形式:
![]()
式(2.18)以向量x为未知元,它的解称为方程组(2.3)的解向量.若把系数矩阵A按行分成m块,则线性方程组Ax=b可记作
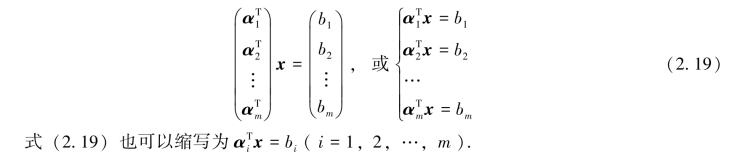
若把系数矩阵A按列分成n块,则线性方程组Ax=b可记作
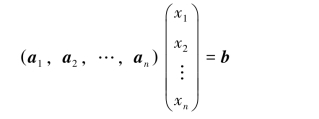
即
![]()
式(2.18)、式(2.19)和式(2.20)是线性方程组(2.3)的三种变形,它们与式(2.3)等同使用而不加区分,并都称为线性方程组或线性方程,而解与解向量也不加区别.
下面给出第一章中的定理1.7.1,即克拉默法则的证明.
证明 把式(1.13)写成矩阵方程:
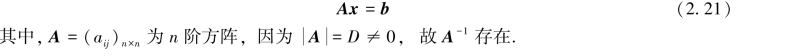
令x=A-1b,则有
![]()
表明x=A-1b是方程组(2.21)的解向量.
由Ax=b,有A-1Ax=A-1b,即x=A-1b,根据逆矩阵的唯一性可知,x=A-1b是方程组(2.21)的唯一的解向量.