2.2.4 矩阵的转置
2026年01月14日
2.2.4 矩阵的转置
定义2.2.4 设有m×n矩阵:
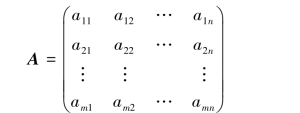
将A的行换成同序数的列所得到的n×m矩阵
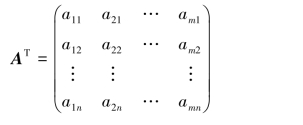
称为矩阵A的转置矩阵.
矩阵的转置运算满足以下运算律(假设运算都是可行的):
(1)(AT)T=A;
(2)(A+B)T=AT+BT;
(3)(λA)T=λAT;
(4)(AB)T=BTAT.
这里仅证明(4).设A=(aij)m×s,B=(bij)s×n,记AB=C=(cij)m×n,BTAT=D=(dij)n×m.则(AB)T的第i行第j列位置上的元素,即原矩阵AB的第j行第i列位置上的元素,它是
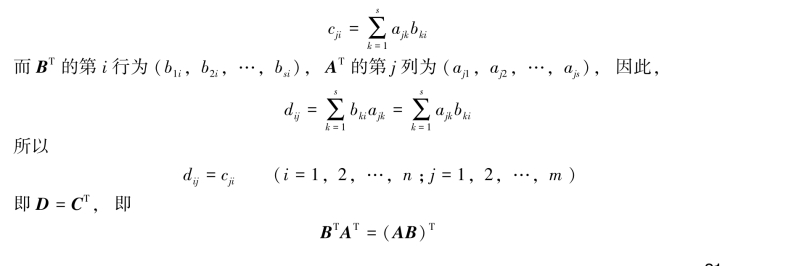
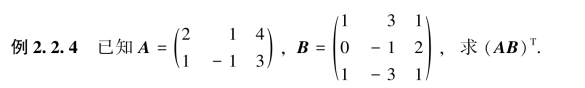
解法1 因为(https://www.daowen.com)
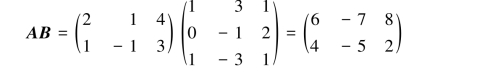
所以
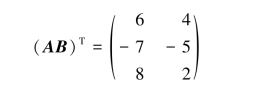
解法2
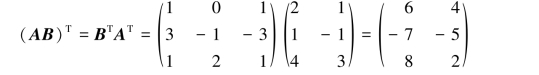
设A为n阶方阵,若满足AT=A,即aij=aji(i,j=1,2,…,n),则称A为n阶对称矩阵,简称对称阵.对称阵的特点:它的元素以主对角线为对称轴对应相等.
若方阵A满足AT=-A,即
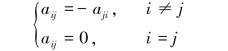
则称A为n阶反对称矩阵.
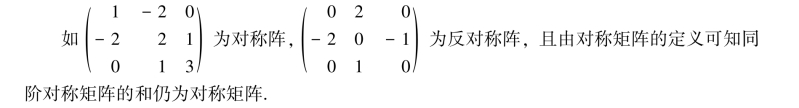
例2.2.5 已知A是对称阵,B是反对称阵,即AT=A,BT=-B,求证:(1)B2是对称阵;(2)AB+BA是反对称阵.
证明 (1)因(B2)T=(BB)T=BTBT=(-B)(-B)=B2,故B2是对称阵.
(2)因(AB+BA)T=(AB)T+(BA)T=BTAT+ATBT=-BA+A(-B)=-(AB+BA),故AB+BA是反对称阵.
