6.1.2 线性空间的基与维数
定义6.1.3 设V是实数域R上的一个线性空间,若V中存在n个元素α1,α2,…,αn,满足:
(1)α1,α2,…,αn线性无关;
(2)V中任一元素α总可由α1,α2,…,αn线性表示.
那么,称α1,α2,…,αn为线性空间V的一个基,称n为线性空间V的维数,记作dimV=n.
注意:只含有一个零元素的线性空间没有基,规定它的维数是0.
维数为n的线性空间称为n维线性空间,记作Vn.如果一个线性空间V中有任意多个线性无关的向量,那么称V为无限维的线性空间.而n维线性空间则统称为有限维的线性空间.本书主要讨论有限维的线性空间.
设α1,α2,…,αn是Vn的一个基,对于∀α∈Vn,存在唯一的一组有序数组x1,x2,…,xn,使得
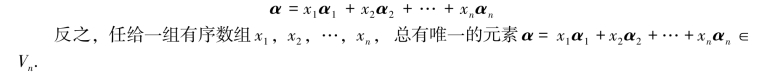
即Vn中的向量α与有序数组(x1,x2,…,xn)T构成一一对应的关系,所以α可以用有序数组(x1,x2,…,xn)T表示.
定义6.1.4 设α1,α2,…,αn是线性空间Vn的一个基,对于任一元素α∈Vn,有且仅有一组有序数x1,x2,…,xn,使得
![]()
称有序数组x1,x2,…,xn为元素α在基α1,α2,…,αn下的坐标,记作α=(x1,x2,…,xn)T.
定理6.1.1 设Vn为实数域R上的n维线性空间,则Vn中任意k(k<n)个线性无关向量α1,α2,…,αk必可扩充成Vn的一个基.
证明 因k<n,故α1,α2,…,αk不是V的基,因此V中至少有一个非零向量αk+1不可由这组向量线性表出,因而向量组α1,α2,…,αk,αk+1线性无关.若k+1=n,则上面这个向量组可作为V的基.若k+1<n,则同样可得一非零向量αk+2,使向量组α1,α2,…,αk,αk+1,αk+2线性无关.若k+2=n,则这个向量组可作为V的基.若k+2<n,则重复用同样的方法,注意到n为有限数,故经过n-k次后,总可找到向量αk+1,αk+2,…,αn,使向量组α1,α2,…,αk,αk+1,αk+2,…,αn线性无关,从而成为V的一个基.
设

由于ε1,ε2,…,εn是Rn中n个线性无关的向量,因此是Rn的一个基.对于向量α=(a1,a2,…,an)T,有
![]()
因此,α在基ε1,ε2,…,εn下的坐标为(a1-a2,a2-a3,…,an)T.
例6.1.3 线性空间P[x]n中任何一个多项式p(x)都可以用n个多项式1,x,x2,…,xn-1线性表示.设P[x]3中的两个基分别为
(1)p1=1,p2=x,p3=x2,p4=x3;
(2)q1=1,q2=2+x,q3=3x2,q4=2x3.
求多项式p=4x3+6x2+3x+1在这两个基下的坐标.
解 因为p=p1+3p2+6p3+4p4,所以p在基(1)下的坐标为(1,3,6,4)T.又因为p=-5q1+3q2+2q3+2q4,所以p在基(2)下的坐标为(-5,3,2,2)T.
此例说明同一个多项式在不同基下的坐标是不同的.
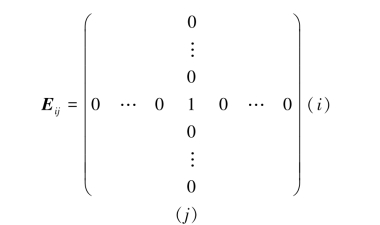
例6.1.4 设Rm×n是实数域R上的m×n阶矩阵所构成的线性空间,考虑如下的m×n个矩阵
 (https://www.daowen.com)
(https://www.daowen.com)
即Eij(i=1,2,…,m;j=1,2,…,n)里除了第i行第j列位置上的元素为1外,其他元素全部为零.根据矩阵的加法和数乘矩阵运算,每个m×n矩阵都可以表示成
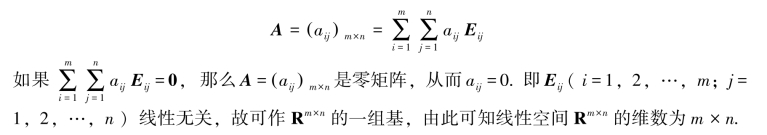
定义6.1.5 设W是实数域R上线性空间V的一个非空子集,如果W对于V的加法和数乘运算也构成线性空间,那么称W为V的一个线性子空间,简称子空间.
定理6.1.2 设W是实数域R上的线性空间V的非空子集合,如果W对于V的加法和数乘运算是封闭的,即对于∀α,β∈W,有α+β∈W,对于∀α∈W,k∈R,有kα∈W,那么W是V的一个子空间.
证明 由于W对于V的两种运算是封闭的,因此W中有加法和数乘运算,又因为定义6.1.1中第(1)、(2)、(5)、(6)、(7)、(8)条在V中对于任一元素成立,自然对于W的元素也成立.下面验证第(3)、(4)条在W中也成立,由W对于数乘运算的封闭性,知α∈W,0=0α∈W,所以V中的零向量也是W的零向量,并且-α=(-1)α∈W,因此条件(3)、(4)也成立,故W是V的一个子空间.
线性空间V本身是它自己的子空间;一个零元素的集是一个线性空间,称为零空间,它也是线性空间的子空间,称V本身和零空间为平凡子空间.V的非平凡子空间称为真子空间.
定理6.1.3 数域R上的线性空间V的非空子集合W是V的一个子空间的充要条件是对于任意k,l∈R和任意α,β∈W,有kα+lβ∈W.
证明 必要性.由于W是V的子空间,那么W对于数乘运算封闭,所以对于k,l∈R,α,β∈W,有kα∈W,lβ∈W;又因为W对于V的加法封闭,所以kα+lβ∈W.
充分性.如果对于任意k,l∈R和任意α,β∈W,有kα+lβ∈W,取k=l=1,则有α+β∈W,取l=0,有kα∈W,即W对于V的加法和数乘运算封闭.
例6.1.5 设A∈Rm×n,齐次线性方程组Ax=0的全部解向量构成n维线性空间Rn的一个子空间.这个子空间称为齐次线性方程组的解空间或矩阵A的零空间(或核),记为N(A)(或Ker(A)).因为解空间的基就是齐次线性方程组的基础解系,所以dim(N(A))=n-R(A).
定义6.1.6 设V与V'是实数域R上两个线性空间,如果存在一个V到V'的一一对应关系σ,对于任意两个向量α,β∈V及任意数k∈R,有
(1)σ(α+β)=σ(α)+σ(β);
(2)σ(kα)=kσ(α).
成立,那么称V与V'是同构的.
定理6.1.4 实数域R上任意一个n维线性空间Vn都与Rn同构.
证明 设α1,α2,…,αn是Vn中一组基,α是Vn中任意向量,则
![]()
(m1,m2,…,mn)T是α在这组基下唯一确定的坐标,且(m1,m2,…,mn)T∈Rn,所以在Vn和Rn之间可以建立一一对应关系:
![]()
设β=l1α1+l2α2+…+lnαn∈Vn,则
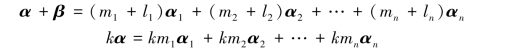
因此
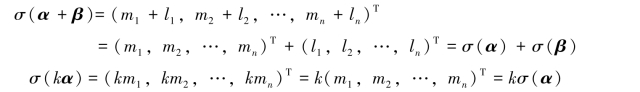
故实数域R上任意一个n维线性空间Vn都与Rn同构.
定理6.1.5 实数域R上两个有限维线性空间同构的充要条件是它们的维数相同.
根据这个定理,实数域R上相同维数的向量空间本质上是一样的.所以Rn可以作为研究n维线性空间的代表.
