1.5.1　行列式的性质

1.5.1　行列式的性质

定义1.5.1　将行列式D行列互换后得到的新行列式称为D的转置行列式,记作DT,即若

性质1.5.1　行列式与它的转置行列式相等.即

证明　令bij=aji,其中i,j=1,2,…,n,则式(1.7)等号右侧为

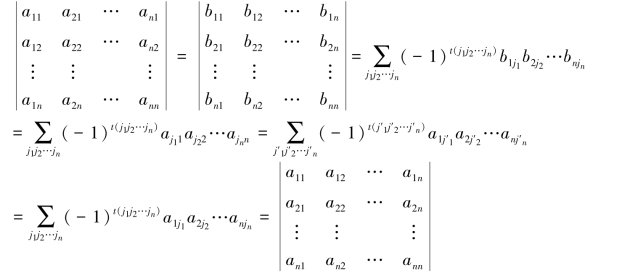
证毕.

由该性质可知,行列式对行成立的性质对列也同样成立.

性质1.5.2　互换行列式的两行(列),行列式反号.即

交换ji和jk的位置,利用对换的性质,进行一次对换排列改变奇偶性得到:

由性质1.5.2容易推得:

性质1.5.3　若行列式的两行(列)对应元素相同,则行列式为零.

性质1.5.4　行列式的一行(列)的所有元素同时乘以一个数k,等于用数k乘以此行列式.

证明　设行列式D1和D2分别为

则有

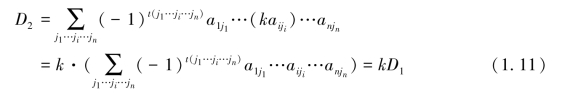
性质1.5.5　行列式的一行(列)的所有元素的公因子k,可以提到行列式的外面.

性质1.5.5是性质1.5.4的一种特殊情况.

性质1.5.6　如果行列式中的一行(列)为零,则行列式为零.

在性质1.5.4中,令k=0,有性质1.5.6.

性质1.5.7　如果行列式中的两行(列)成比例,则行列式为零.

综合性质1.5.3和性质1.5.5可以得出性质1.5.7的结论.

性质1.5.8　如果行列式的一行(列)的元素是两个数的和,则该行列式可以分解成两个行列式的和.

证明　由n阶行列式的定义得

性质1.5.9　把行列式的某一行(列)的各元素的k倍加到另一行(列)对应的元素中,行列式的值不变.

综合性质1.5.7和性质1.5.8,可以得出性质1.5.9的结论.

规定:以ri(ci)表示行列式的第i行(列).交换i,j两行(列)记为ri↔rj(ci↔cj),第i行(列)乘以k记为ri×k(ci×k),以数k乘以j行(列)加到第i行(列)记为ri+krj(ci+kcj).