3.3.2 向量组的线性相关性判定
定理3.3.1 设α1,α2,…,αn∈Rm,则
(1)α1,α2,…,αn线性相关的充分必要条件是存在某个αi(i=1,2,…,n)可被其余向量线性表示;
(2)α1,α2,…,αn线性无关的充分必要条件是任一αi(i=1,2,…,n)不能被其余向量线性表示.
证明 由于(1)、(2)两个命题等价,故这里只证(1).
(1)先证必要性.由于α1,α2,…,αn线性相关,故存在不全为零的n个数k1,k2,…,kn∈R,使得
![]()
不妨设某个ki≠0,则有
![]()
再证充分性.如果某个αi可被其余向量线性表示,即存在k1,…,ki-1,ki+1,…,kn∈R,使得
![]()
则
![]()
于是α1,α2,…,αn线性相关.证毕
由定义3.3.1知,向量组A:a1,a2,…,an∈Rm构成矩阵Am×n=(a1,a2,…,an),向量组A线性相关,就是齐次线性方程组(3.2)有非零解,由2.7节定理2.7.1可得如下定理.
定理3.3.2 向量组A:a1,a2,…,an∈Rm线性相关的充分必要条件是其所构成矩阵A=(α1,α2,…,αn)的秩小于向量个数n,向量组线性无关的充分必要条件是R(A)=n.
特别地,若向量组A:a1,a2,…,an∈Rn,此时构成的矩阵An=(a1,a2,…,an)为方阵,即齐次线性方程组(3.2)方程个数与未知数个数相等,由克拉默法则的推论1.7.1可得如下推论.

解法1(定理法) 设A=(a1,a2,a3),即
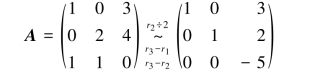
因为R(A)=3,所以由定理3.3.2知,a1,a2,a3线性无关.
解法2(推论法) 因为
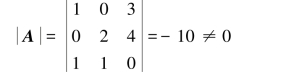 (https://www.daowen.com)
(https://www.daowen.com)
根据推论3.3.1知,a1,a2,a3线性无关.
例3.3.2 已知α1,α2,α3线性无关,β1=α1+α2,β2=α2-α3,β3=α3-α1,证明β1,β2,β3线性无关.
证明 设x1β1+x2β2+x3β3=0,即
![]()
因为α1,α2,α3线性无关,故
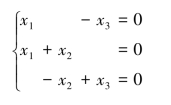
设其系数矩阵为A,则
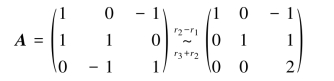
即R(A)=3,从而x1=x2=x3=0,所以β1,β2,β3线性无关.
定理3.3.3 设向量组A:a1,a2,…,at∈Rm线性相关,存在at+1,at+2,…,at+s∈Rm,则向量组B:a1,a2,…,at,at+1,at+2,…,at+s也线性相关.反之,若向量组B线性无关,则向量组A也一定线性无关.
证明 由于向量组A线性相关,因此有不全为零的数k1,k2,…,kt∈R,使
![]()
从而有
![]()
故向量组B也线性相关.反之亦然.

证明 记Ar×n=(α1,α2,…,αn),B(r+s)×n=(β1,β2,…,βn),有R(A)≤R(B),若向量组A线性无关,则R(A)=n,从而有R(B)≥n,但R(B)≤n(因为B只有n列),故R(B)=n,所以向量组B线性无关.反之亦然.
定理3.3.5 设α1,α2,…,αn线性无关,α1,α2,…,αn,β线性相关,则β能由α1,α2,…,αn线性表示,且表示式是唯一的.
证明 记A=(α1,α2,…,αn),B=(α1,α2,…,αn,β),有R(A)≤R(B),因为向量组A线性无关,则R(A)=n,而向量组B线性相关,从而有R(B)<n+1,所以n≤R(B)<n+1,即有R(A)=R(B)=n,所以由方程组解的理论知β能由α1,α2,…,αn线性表示,且表示式是唯一的.
定理3.3.6 当n>m时,n个m维向量必线性相关.
证明 n个m维向量构成的向量组a1,a2,…,an构成的矩阵Am×n=(α1,α2,…,αn),有R(A)≤m,由题意知n>m,则R(A)<n,由定理3.3.2知向量组a1,a2,…,an线性相关.
