本章小结

本章主要讨论方阵的特征值与特征向量、方阵的相似对角化和二次型及其标准形等问题.这一章是前面各章知识的综合应用,综合性较强,掌握起来有一定的难度.通过对本章的学习我们应该着重掌握如下内容:

理解方阵的特征值与特征向量的概念与性质,并掌握其求法.要注意到求矩阵的特征值实质上是计算行列式的问题,而求特征值所对应的特征向量实质上就是求齐次线性方程组的非零解.这样就把特征值与特征向量的计算问题转化为前面各章知识的应用.

了解相似矩阵的概念与性质.了解n阶方阵对角化的常用条件:有n个线性无关的特征向量(充要条件);有n个互不相同的特征值或实对称矩阵(充分条件).掌握实对称矩阵通过正交相似变换化为对角矩阵.

了解二次型及其矩阵表示.掌握用正交变换法化二次型为标准形的方法.利用正交变换法化二次型为标准形问题实质上与对称矩阵正交相似(亦合同)于对角矩阵是一个问题的两种提法,认清这一点将有助于本章内容的融会贯通.了解惯性定理、二次型的秩、二次型的正定性,并能够利用特征值和赫尔维茨定理两种方法判别二次型正定性.

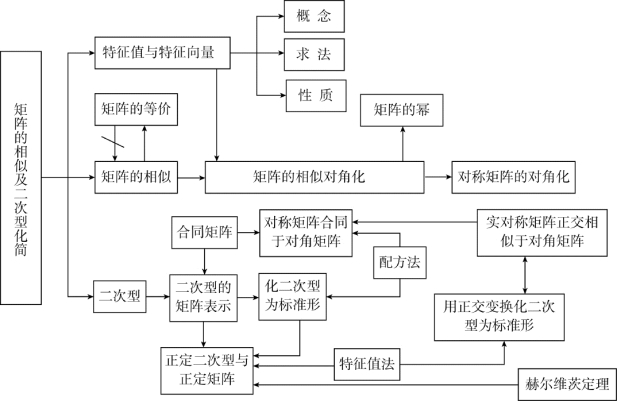
本章知识结构图如下: