2.6.1　矩阵的秩的概念

定义2.6.1　在m×n矩阵A中,任取k行与k列(k≤m,k≤n),位于这些行列交叉处的k2个元素,不改变它们在A中所处的位置次序而得的k阶行列式,称为矩阵A的k阶子式.

m×n矩阵A的k阶子式共有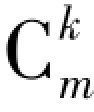·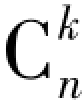个.定义2.6.2　设在矩阵A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在的话)全等于0,则称D为矩阵A的最高阶非零子式,数r称为矩阵A的秩,记作R(A).并规定零矩阵的秩等于0.

由行列式按行(列)展开的性质可知,在A中当所有r+1阶子式全等于0时,所有高于r+1阶的子式也全等于0,因此矩阵A的秩R(A)就是A的非零子式的最高阶数.

由于R(A)是A的非零子式的最高阶数,因此若矩阵A中有某个s阶子式不为0,则R(A)≥s;若A中所有t阶子式全为0,则R(A)＜t.

若A为m×n矩阵,则0≤R(A)≤min{m,n}.

由于行列式与其转置行列式相等,因此显然有R(AT)=R(A).