§5.6 用配方法化简二次型为标准形
任何实二次型都能用正交变换化为标准形,结果简洁,具有保持几何形状不变的特点.但是,因其计算量大,化简过程复杂,有时,可以采用一般的可逆线性变换对二次型进行化简.例如,在用二次型求连续可微多元函数的极值时,可以采用可逆线性变换化简问题,而不必使用正交变换.本节讨论用可逆线性变换化二次型为标准形的配方法.
配方法也叫拉格朗日(Lagrange)配方法,具有试探性和灵活性的特点.所谓配方法,是通过变形的技巧获得合同可逆线性变换来化简二次型的一种方法.
配方法的做法是,根据二次型的结构特点,对二次型进行变形处理,实现化简.
情形1 当二次型(5.8)中含有变量xi的平方项时,把含有变量xi的各项集中,按照xi配成完全平方项.依次对其他的变量进行配方,直到二次型的表达式成为平方项之和的形式.建立“新老”变量之间的关系,得到可逆的线性变换矩阵.化简的方法不唯一.
情形2 当二次型(5.8)中不含有变量xi的平方项时,需要先对某个aij≠0(i≠j)作一个预备的可逆线性变换:
使二次型化为关于变量yi的形式并出现关于yi的平方项,再按照情形1进行配方.最后,经过两次可逆线性变换,化二次型为标准形.
下面通过例题说明用配方法化简二次型.
例5.6.1 用配方法求一个可逆线性变换矩阵,化二次型
为标准形.
解 由于所给的二次型中含有变量x1的平方项,先合并含x1的项并对x1进行配方:
例5.6.2 用配方法化二次型f(x1,x2,x3)=2x1x2+2x1x3-6x2x3为规范形,并求所用的可逆线性变换.
解 所给的二次型中不含平方项,先对乘积项x1x2作预备的可逆线性变换,产生平方项,并将二次型化为关于变量yi的形式:
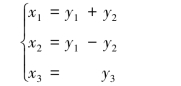
代入二次型f(x1,x2,x3)=2x1x2+2x1x3-6x2x3,得
再进行配方:
得可逆线性变换矩阵为
