4.2.3 初等行变换求非齐次线性方程组通解的方法
定理4.2.1给出了一种求非齐次线性方程组Ax=b的通解的方法.即先求出对应的齐次线性方程组Ax=0的基础解系ξ1,ξ2,…,ξn-r,再求一个非齐次线性方程组Ax=b的特解η*,则x=k1ξ1+k2ξ2+…+kn-rξn-r+η*(k1,k2,…,kn-r为任意常数)即为非齐次线性方程组Ax=b的通解.
通常,基础解系ξ1,ξ2,…,ξn-r和特解可以通过对增广矩阵作初等行变换化为行最简形矩阵来求得.下面通过例子来说明.
例4.2.1 求解非齐次线性方程组:
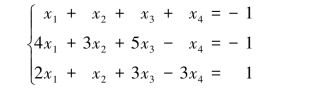
解 对方程组的增广矩阵作如下初等行变换:
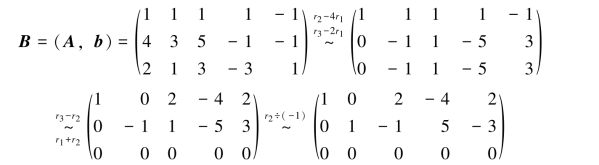
由R(A)=R(B)=2＜4,知方程组有无穷多解,且原方程组所对应的同解方程组为
即得对应的齐次线性方程组的基础解系:
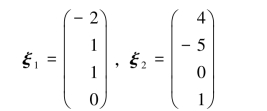
于是,所求通解为
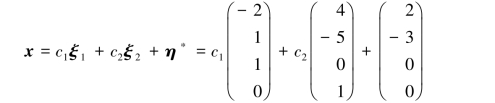
其中,c1,c2为任意实数.
例4.2.2 设四元非齐次线性方程组Ax=b的系数矩阵A的秩为3,已知它的三个解向量为η1,η2,η3,其中
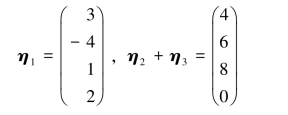
求该方程组的通解.
解 依题意,方程组Ax=b的对应的齐次线性方程组Ax=0的基础解系含有4-3=1个向量.于是,Ax=0的任何一个非零解都可作为其基础解系.显然
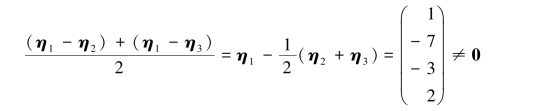
是对应的齐次线性方程组Ax=0的非零解,可作为其基础解系.因此,方程组Ax=b的通解为
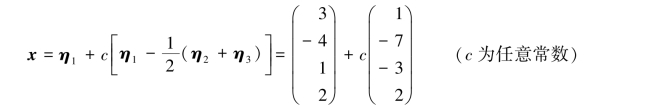
例4.2.3 λ取何值时,线性方程组
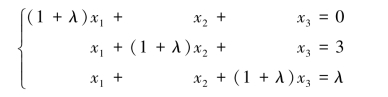
(1)有唯一解;(2)无解;(3)有无穷多个解,并在有无穷多解时,求出通解.
解法1 对增广矩阵B=(A,b)作初等行变换把它变为行阶梯形矩阵,有
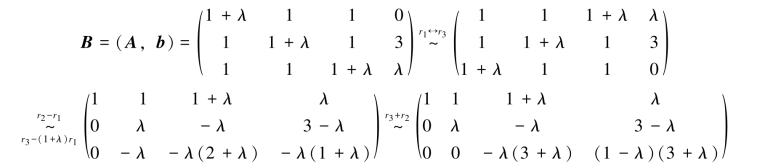
(1)当λ≠0且λ≠-3时,R(A)=R(B)=3,方程组有唯一解;
(2)当λ=0时,R(A)=1,R(B)=2,方程组无解;
(3)当λ=-3时,R(A)=R(B)=2＜3,方程组有无穷多解,这时有
R(A)=1,R(B)=2,系数矩阵的秩与增广矩阵的秩不等,故方程组无解;
(3)当λ=-3时,增广矩阵为
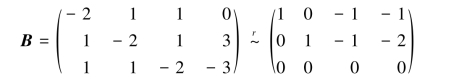
R(A)=R(B)=2＜3,方程组有无穷多个解.
由同解方程组:
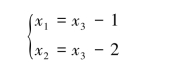
得通解为3
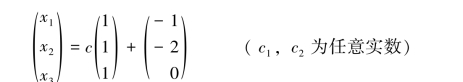
比较解法1与解法2,显见解法2较简单.但解法2的方法只适用于系数矩阵为方阵的情形.
例4.2.4 已知平面上三条不同直线的方程分别为
试证明这三条直线交于一点的充分必要条件为a+b+c=0.
证明 三条平面直线交于一点的充分必要条件是由这三条直线的方程联立所得的二元线性方程组有唯一解,而它有唯一解的充分必要条件是系数矩阵的秩与增广矩阵的秩都等于2.
必要性.设三条直线l1,l2,l3交于一点,则二元线性方程组
图4.1