4.1.2 齐次线性方程组的解空间、基础解系及通解结构
把方程(4.2)的全体解所组成的集合记作S.显然它是非空集合,且由性质4.1.1、4.1.2可得:
(1)若ξ1,ξ2∈S,则ξ1+ξ2∈S;
(2)若ξ1∈S,k∈R,则kξ1∈S.
上述结论说明集合S对向量的加法和数乘两种运算是封闭的,所以集合S构成一个向量空间,称为齐次线性方程组(4.1)的解空间.
下面讨论解空间的维数及基.
设系数矩阵A的秩为r,不妨设A的前r个列向量线性无关,于是A经过初等行变换化为行最简形矩阵:

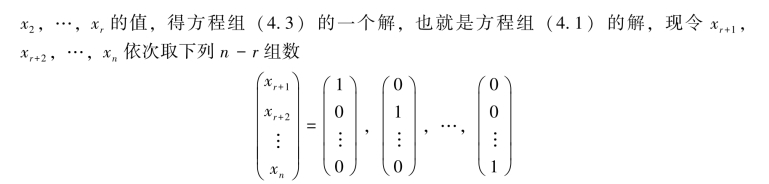
由方程组(4.3)依次可得
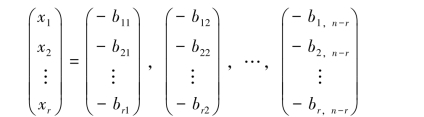
从而求得方程组(4.1)的n-r个解:
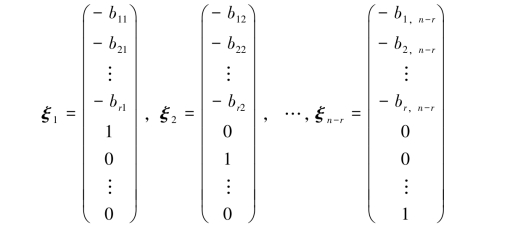
下面证明ξ1,ξ2,…,ξn-r就是解空间S的一个基.
(1)由于ξ1,ξ2,…,ξn-r的后n-r个分量构成的向量组
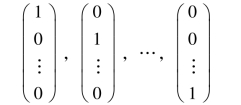
线性无关,因此由第3章定理3.3.4知,在每个向量前面添加r个分量而得到的n-r个n维向量ξ1,ξ2,…,ξn-r也线性无关.

由于ξ1,ξ2,…,ξn-r是方程组(4.1)的解,故η也是方程组(4.1)的解.比较η和ξ知,它们的后n-r个分量对应相等,因为它们都满足方程组(4.3),从而它们的前r个分量亦对应相等,因此ξ=η.即
![]()
综上知,ξ1,ξ2,…,ξn-r是解空间S的一个基,S的维数是n-r.
定义4.1.1 齐次线性方程组Ax=0的解空间S的基称为该方程组的基础解系.
由上述分析可得如下定理.
定理4.1.1 设m×n矩阵A的秩R(A)=r,则n元齐次线性方程组Ax=0的解空间S的维数为n-r.
当R(A)=n时,方程组Ax=0有唯一解即零解,这时解空间S只含零向量,没有基础解系;
当R(A)=r<n时,方程组Ax=0有无穷多个解,其基础解系含有n-r个向量,设ξ1,ξ2,…,ξn-r为Ax=0的基础解系,则该方程组的任一解可以表示为
![]()
其中,k1,k2,…,kn-r为任意常数.称式(4.4)为方程组Ax=0的通解.
注意:解空间S的基础解系就是解集S的一个最大线性无关组.因此,基础解系不是唯一的,S中任意n-r个线性无关的解向量均是Ax=0的基础解系.所以方程组Ax=0的通解表达式也不是唯一的.
上面的证明过程提供了一种求齐次线性方程组基础解系的方法,并能清楚地表述Ax=0的通解.
例4.1.1 求齐次线性方程组
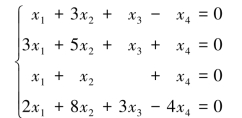
的基础解系与通解.
解 对系数矩阵A作初等行变换,化为行最简形矩阵:

得到原方程组的同解方程组为
 (https://www.daowen.com)
(https://www.daowen.com)
并由此得到通解:
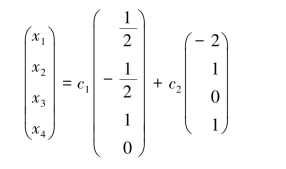
其中,c1,c2为任意实数.
关于Ax=0的通解说明如下:

从而得另一形式的通解:
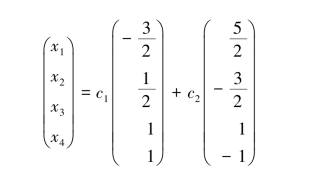
其中,c1,c2为任意实数.显然ξ1,ξ2与η1,η2是等价的,两个通解虽然形式不一样,但都含两个任意常数,且都可表示方程组的任一解.
(2)求基础解系和通解除了上述方法外,还可用2.7节求解齐次线性方程组的方法:将同解方程组式(4.5)化简为
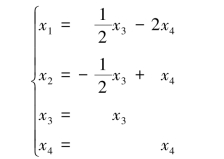
令x3=c1,x4=c2,代入并写成向量的形式,也可得到齐次线性方程组的通解为

(3)上述解法中,由于为行最简形矩阵的结构,故x1总是选为非自由未知数.对于解方程来说,x1当然也可选为自由未知数.如果要选x1为自由未知数,那么就不能采用上述化系数矩阵为行最简形矩阵的“标准程序”,而要稍作变化,对系数矩阵A作初等行变换时,先把其中某一列(不一定是第一列)化为(1,0,0,0)T.如本例中的第四列数值较简,容易化出3个0:
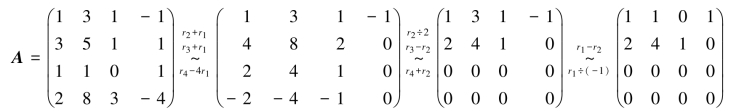
上式最后一个矩阵虽不是行最简形矩阵,但也具备行最简形矩阵的功能.按照这个矩阵,取x1,x2为自由未知量,便可写出通解:
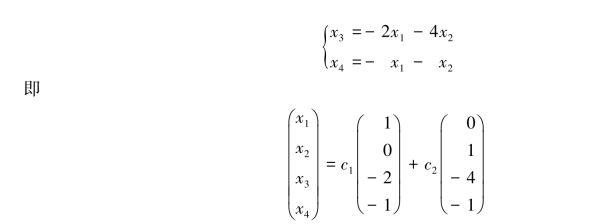
其中,c1,c2为任意实数.

由此可得,自由未知数的个数是确定的(为n-r个),但自由未知数的选取在满足n-r的前提下是任意的.
定理4.1.1不仅是线性方程组各种解法的理论基础,在讨论向量组的线性相关性时也很有用.
例4.1.2 设Am×nBn×l=O,证明:R(A)+R(B)≤n.

例4.1.3 设A为m×n实矩阵,证明:R(ATA)=R(A).
证明 设x为n维列向量,
若x满足Ax=0,则AT(Ax)=0,即(ATA)x=0;
若x满足ATAx=0,xT(ATA)x=0,即(Ax)T(Ax)=0,从而Ax=0.(参看第2章例2.4.2)
综上,方程组Ax=0与(ATA)x=0同解,由定理4.1.1,有R(ATA)=R(A).
例4.1.4 设α1,α2,α3是齐次线性方程组Ax=0的一个基础解系,试证明α1+α2,α2+2α3,α3+3α1也是该方程组的一个基础解系.
证明 一个向量组可以成为齐次线性方程组Ax=0的基础解系,要满足条件:(1)是方程组的解;(2)是线性无关的;(3)所含向量个数(即解空间的维数)为R(S)=n-R(A).由已知条件α1,α2,α3为Ax=0的一个基础解系,有3个解向量,说明解集合S的秩R(S)=3.由解的性质知,α1+α2,α2+2α3,α3+3α1仍是Ax=0的解,故只要证明α1+α2,α2+2α3,α3+3α1线性无关即可证明它们是Ax=0的基础解系.
设k1(α1+α2)+k2(α2+2α3)+k3(α3+3α1)=0,则有
![]()
由于α1,α2,α3线性无关,故得
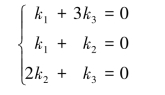
由系数行列式
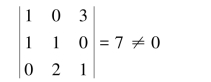
可知k1=k2=k3=0,从而α1+α2,α2+α3,α3+α1线性无关,为基础解系.
