6.3.1 线性变换
线性空间中元素之间的联系反映为线性空间的映射,而从线性空间到另一个线性空间的线性映射在数学中扮演着重要的角色.
定义6.3.1 设有两个非空集合A,B,如果对于任一元素a∈A,按照一定规则,总有一个确定的元素b∈B和它对应,那么称这个对应规则为从集合A到集合B的映射,记作T,并记b=T(a),或b=Ta(a∈A).并说映射T把元素a变为b,b称为a在映射T下的像,a称为b在映射T下的源,A称为映射T的源集,像的全体所构成的集合称为像集,记作T(A),即
![]()
由定义可以看出T(A)⊂B.映射的概念实际上是函数概念的推广.
定义6.3.2 设Vn,Um分别是实数域R上的n维和m维线性空间,T是一个从Vn到Um的映射,如果映射T满足:
(1)任给α1,α2∈Vn,有T(α1+α2)=T(α1)+T(α2);
(2)任给α∈Vn,k∈R,都有T(kα)=kT(α).
那么称T为从Vn到Um的线性映射或线性变换.
由定义可以看出线性映射就是保持线性组合的对应的映射.若Um=Vn,那么T是一个从线性空间Vn到其自身的线性变换,称为线性空间Vn中的线性变换.
本书主要讨论线性空间Vn中的线性变换.
性质6.3.1 线性空间V中的恒等变换或称单位变换E,即
![]()
以及零变换0,即
![]()
都是线性变换.
例6.3.1 考虑线性映射L,定义为
![]()
其中,x∈R2.因此,若x=(x1,x2)T,则L(x)=(x1,0)T.试证明L是线性变换.
证明 任取y=(y1,y2)T,k∈R,则
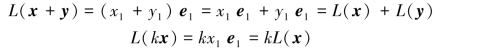
所以L是线性变换.
例6.3.2 在线性空间P[x]3中,
(1)证明微分运算D是一个线性变换;
(2)任取p=a3x3+a2x2+a1x+a0∈P[x]3,定义T(p)=a0,证明T是一个线性变换;定义T1(p)=1,证明T1是个变换,但不是线性变换.
证明 (1)显然微分运算D是P[x]3的一个变换,任取
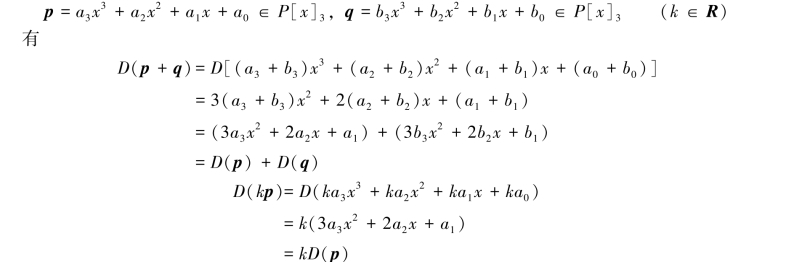
故D是P[x]3中的线性变换.
(2)显然T是P[x]3的一个变换,因为T(p+q)=a0+b0=T(p)+T(q);T(kp)=ka0=kT(p),故T是P[x]3中的线性变换.
显然T1是P[x]3的一个变换,但因为T1(p+q)=1,而T1(p)+T1(q)=1+1=2,所以T1(p+q)≠T1(p)+T1(q),故T1不是P[x]3的线性变换.
由定义6.3.2不难推得下面线性变换的简单性质:
(1)设T是V上的线性变换,则T(0)=0,T(-α)=-T(α);
(2)若β=k1α1+k2α2+…+knαn,则T(β)=k1T(α1)+k2T(α2)+…+knT(αn);
(3)若α1,a2,…,αm线性相关,则T(α1),T(α2),…,T(αm)亦线性相关,即线性变换把线性相关的向量组变成线性无关的向量组;(https://www.daowen.com)
但是应该注意,性质(3)的逆不成立,线性变换可能把线性无关的向量组也变成线性相关的向量组.
(4)线性变换T的像集T(Vn)是一个线性空间,称为线性变换T的像空间;
事实上,如果β1,β2∈T(Vn),则有α1,α2∈Vn,使得T(α1)=β1,T(α2)=β2,从而
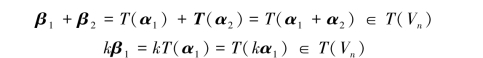
由此可知,T(Vn)对Vn中的加法和数乘运算封闭,因此T(Vn)是一个线性空间.
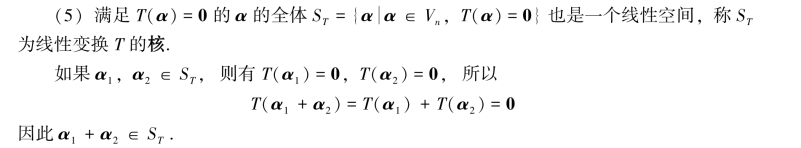
若α1∈ST,k∈R,则T(kα1)=kT(α1)=0,所以kα1∈ST.
由此可知,ST对Vn中的加法和数乘运算封闭,因此ST也是一个线性空间.
T(Vn)的维数称为T的秩,记为rank(T),ST的维数称为T的零度,记为nullity(T).
定理6.3.1 设T是n维线性空间Vn的一个线性变换,则
![]()
例6.3.3 设有n阶矩阵:
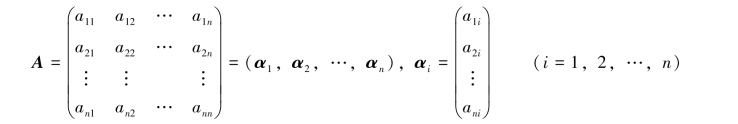
Rn中的变换T:T(x)=Ax(x∈Rn),为线性变换.T的像空间就是由α1,α2,…,αn所生成的向量空间:
![]()
T的核ST就是齐次线性方程组Ax=0的解空间.
试用L(V)表示线性空间V中所有线性变换所组成的集合.
设T1,T2∈L(V),对于每个α∈V,定义线性变换的加法:
![]()
称T1+T2为T1与T2的和,易知T1+T2∈L(V),即T1+T2还是线性变换.
设T∈L(V),k∈R,对于每个α∈V,定义数与线性变换的乘法:
![]()
易知kT∈L(V),即kT还是线性变换.
可以证明线性空间V上的所有变换L(V),对于如上定义的加法和数与线性变换的乘法运算构成数域R上的一个线性空间.
定理6.3.2 设α1,α2,…,αn是线性空间Vn的一个基,β1,β2,…,βn是Vn中任意n个向量,则存在唯一的线性变换T,使得
![]()

因此,T是线性变换.由于
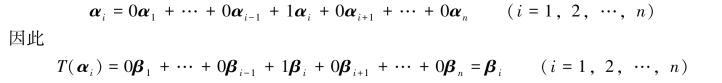
再证明唯一性.如果还有一个线性变换S,使得
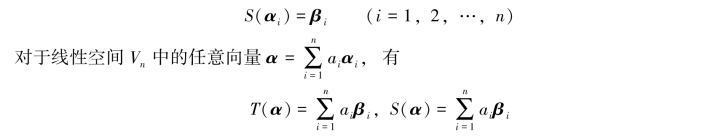
从而T(α)=S(α),即T=S.
由此定理说明一个线性变换完全被它在一个基上的作用所决定,所以可以建立下面的线性变换与矩阵的联系.
