二、典型例题解析
解 编程及运行结果如下:
注意:(1)通常,在求行列式的值时也是先将其元素录入一个矩阵,再运用det()函数求值.
(2)在求矩阵B的秩时,也可以将B化为行最简行矩阵,然后观察其非零行的个数,从而确定R(B),命令如下:
(3)poly(B)命令计算的是矩阵B的特征多项式的系数,由MATLAB运算结果可知B的特征多项式为:x3-4x2-21x-20.此外,运用符号运算工具箱中的poly()函数同样可以求出矩阵的特征多项式,如
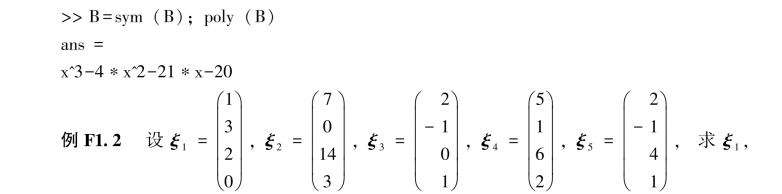
ξ2,…,ξ5组成矩阵的秩和一个最大无关组,并把不属于最大无关组的列向量用最大无关组线性表示.
解 编程如下:
由结果可知,最简矩阵第1列、第2列和第3列向量线性无关,所以对应于原矩阵A的前三个行向量线性无关,即原向量组中一个最大无关组为ξ1,ξ2和ξ3.
解 编程如下:
解 编程如下:
解 方阵A可以对角化的充分必要条件是它的几何重数等于代数重数,即满足A的特征值λ的几何重数为方程组(A-λE)x=0的解空间的维数.按照此思想,编写函数panduankeduijiaohua.m文件如下:
给定一个矩阵A,在MATLAB运行环境界面调用函数panduankeduijiaohua(A),若返回值为1,则A可对角化;若返回值为0,则A不可对角化.
判断题中给定的A是否可对角化:
但由于所求特征向量所构成矩阵P不是正交矩阵,因此我们再调用orth()命令将其正交化:
解 编程如下:
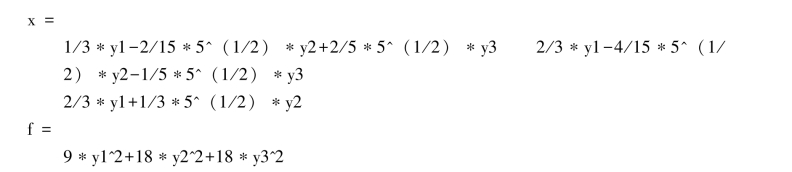
由标准形知:f(x1,x2,x3)=0应该表示椭球面.
下面通过画图验证f(x1,x2,x3)=0表示椭球面的结论:
其图形如附图1.1所示,显然f(x1,x2,x3)=0表示椭球面.
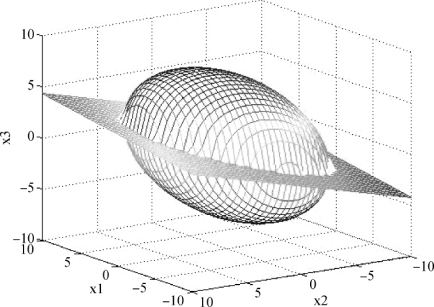
附图1.1
注意:此程序中没有考虑半正定或半负定判断的情形,读者可以仿照此例将其完善.
调用函数panduanyoudingxing(A)重新判断A的有定型:
因此A为不定二次型.
例F1.8 在线性空间R3中,取两个基:
(1)α1=(1,0,1)T,α2=(1,1,0)T,α3=(0,1,1)T;
(2)β1=(1,0,3)T,β2=(2,2,2)T,β3=(-1,1,4)T.
用MATLAB求由基(1)到基(2)的过渡矩阵,设α在基(1)下的坐标为(1,1,3)T,求α在基(2)下的坐标.
解 记U=(α1,α2,α3),V=(β1,β2,β3),a=(1,1,3)T,b为所求坐标.
在MATLAB窗口中输入
