5.1.1　特征值和特征向量的概念

5.1.1　特征值和特征向量的概念

可见,λ=1和λ=5是使得Ax=λx有非零解的方阵A的重要数字特征.

定义5.1.1　设A是n阶方阵,如果数λ和n维非零向量x使关系式

成立,那么称λ为方阵A的特征值,称非零向量x为A的对应于特征值λ的特征向量.

定义5.1.2　设A=(aij)n×n是一个n阶方阵,λ是一个变量,矩阵A-λE的行列式

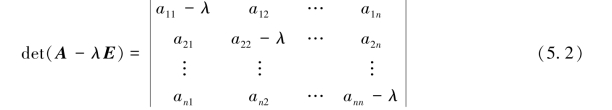
称为A的特征多项式,记作f(λ).这里,f(λ)是一个关于变量λ的n次多项式.

以λ为未知量的方程f(λ)=0,即

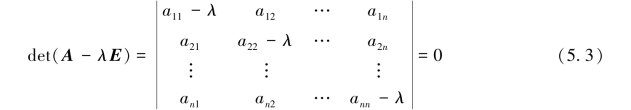
称为矩阵A的特征方程.

针对特征值和特征向量的概念,我们首先要讨论下面的问题:

问题5.1.1　n阶矩阵A的特征值的个数是多少?

问题5.1.2　n阶矩阵A的特征值和其主对角线有什么数量关系?

问题5.1.3　n阶矩阵A的特征值和其行列式有什么数量关系?

问题5.1.4　n阶矩阵A的特征值λ所对应的特征向量是否唯一?

根据多项式理论,一元n次方程f(λ)=0在复数域内有n个根.

设λ1,λ2,…,λn是f(λ)=0的n个根,f(λ)=0的n个根λ1,λ2,…,λn,就是n阶方阵A=(aij)n×n的全部特征值.

由根与系数的关系,有

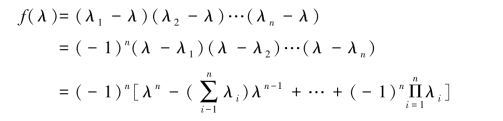
根据行列式理论,可以得到下列结果:

比较λ0的系数关系和λn-1的系数关系,可以回答问题5.1.1~5.1.3,问题5.1.4的回答要用特征值和特征向量的定义式.

问题5.1.1　在复数范围内,f(λ)=0有n个根,即n阶矩阵A的特征值的个数是n.

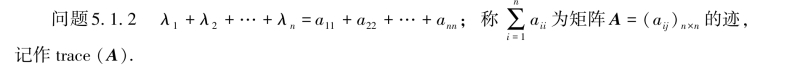
问题5.1.3　λ1λ2…λn=det(A).