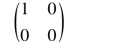§2.1 矩阵的概念
在许多问题中,我们会遇到一些变量用另外一些变量来线性表示的情况.设变量y1,y2,…,ym能用变量x1,x2,…,xn线性表示,即
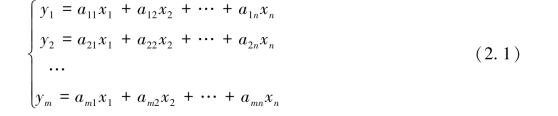
其中,aij为常数(i=1,2,…,m;j=1,2,…,n).这种从变量x1,x2,…,xn到变量y1,y2,…,ym的变换,称为线性变换.
线性变换(2.1)中的系数可以排成m行n列的数表:
含有m个方程、n个变量的线性方程组
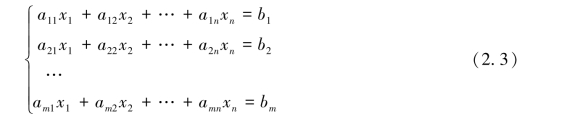
的系数也可以排成这样的数表,这种数表就是本节要研究的矩阵.
定义2.1.1 由m×n个数aij(i=1,2,…,m;j=1,2,…,n)排成m行n列的数表,如式(2.2),为表示它是一个整体,总是加一个括弧,并用大写黑体字母表示,记作
称其为m行n列矩阵(matrix),简称m×n矩阵.这m×n个数称为矩阵A的元素,aij表示矩阵A的第i行第j列的元素.式(2.4)也可简记为
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵.本书中的矩阵除特别说明外,都是指实矩阵.矩阵就是按指定位置储存数据的表,产品产量统计表、学生成绩表等都可以用矩阵来刻画.
当m=n时,A称为n阶方阵,也记作An.
只有一行的矩阵
称为行矩阵,又称行向量.为避免元素间的混淆,行矩阵也记作
只有一列的矩阵
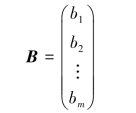
称为列矩阵,又称列向量.
当两个矩阵的行数相等、列数也相等时,称它们是同型矩阵.若A=(aij)与B=(bij)是同型矩阵,且它们的对应元素相等,即
则称矩阵A与B相等,记作
元素都是零的矩阵称为零矩阵,记作O.注意不同型的零矩阵是不同的,因此,零矩阵常记作
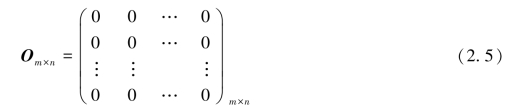
给定了线性变换(2.1),它的系数所构成的矩阵(称为系数矩阵)也就确定了.反之,如果给出一个矩阵作为某个线性变换的系数矩阵,则该线性变换也就确定了.从这个意义上讲,线性变换与矩阵之间存在着一一对应的关系.因此,可以利用矩阵来研究线性变换,也可利用线性变换来解释矩阵的含义.
定义2.1.2 线性变换
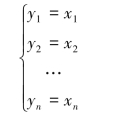
称为恒等变换.它所对应的矩阵称为n阶单位矩阵,简称单位阵,记作
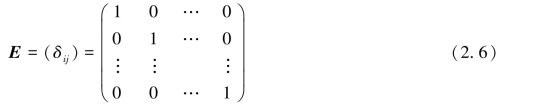
其中,δij为Kronecker运算符号,即
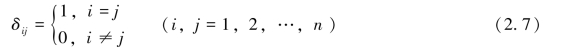
定义2.1.3 线性变换
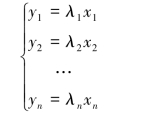
对应n阶方阵
这种主对角线以外的元素都是零的矩阵,称为对角矩阵.对角矩阵也记作
线性变换
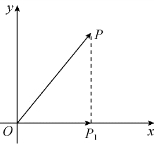
图2.1
线性变换(2.9)可写成
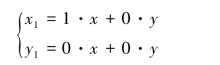
其系数对应的矩阵为
