2.5.1 矩阵的初等变换
矩阵的初等变换是矩阵的一种非常重要的运算,它在解线性方程组、求逆矩阵及矩阵理论的研究中起着重要的作用.为引进矩阵的初等变换,先来分析用消元法解n阶线性方程组的例子.
引例 求解线性方程组

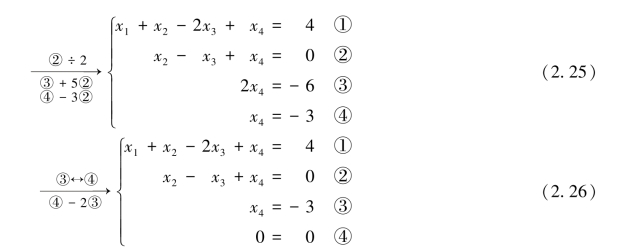
这里方程组(2.22)→方程组(2.23)是为消x1作准备.方程组(2.23)→方程组(2.24)是保留式①中的x1,消去式②,式③,式④中的x1.方程组(2.24)→方程组(2.25)是保留式②中的x2,并把它的系数变为1,然后消去式③,式④中的x2,与此同时,恰好把x3也消去了.方程组(2.25)→方程组(2.26)是消去x4,与此同时恰好把常数也消去了,得到恒等式0=0(若常数不能消去,则会得到矛盾方程0=1,从而说明方程组无解).至此,消元完毕.
方程组(2.26)是含有4个未知数、3个有效方程的方程组,应有一个自由未知数.由于方程组(2.26)呈阶梯形,可把每个台阶的第一个未知数(即x1,x2,x4)选为非自由未知数,剩下的x3选为自由未知数.这样,就只需用“回代”的方法即可求出解,由式③得x4=-3;把x4=-3代入式②,得x2=x3+3;把x4=-3,x2=x3+3代入式①,得x1=x3+4,于是有

其中,x3可任意取值.
在上述消元过程中,始终把方程组看作一个整体,即不是着眼于某一个方程的变形,而是着眼于整个方程组变成另一个方程组.其中用到三种变换,即(1)变换方程次序;(2)以不等于0的数乘某个方程;(3)一个方程加上另一个方程的k倍.由于这三种变换都是可逆的,因此变换前的方程组与变换后的方程组是同解的,这三种变换都是方程组的同解变换,所以最后求得的解(2.27)是方程组(2.22)的全部解.
在上述变换过程中,实际上只是对方程组的系数和常数进行了线性运算,未知数并未参与运算.因此,若记方程组(2.22)的增广矩阵为
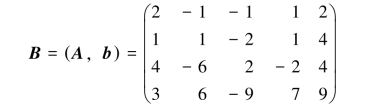
则上述对方程组的变换完全可以转化为对矩阵B的变换.把方程组的上述三种同解变换移植到矩阵上,就得到矩阵的三种初等变换.
定义2.5.1 以下三种变换称为矩阵的初等行变换:
(1)对调两行(对调i,j两行,记作ri↔rj);
(2)以数k≠0乘某一行中的所有元素(第i行乘k,记作ri×k);
(3)把某一行所有元素的k倍加到另一行对应的元素上去(第j行的k倍加到第i行上,记作ri+krj).
把定义中的“行”换成“列”,即得矩阵的初等列变换的定义(所用的记号是把“r”换成“c”).
矩阵的初等行变换与初等列变换,统称为初等变换.

矩阵之间的等价关系具有下列性质.(https://www.daowen.com)
(1)反身性:A~A;
(2)对称性:若A~B,则B~A;
(3)传递性:若A~B,B~C,则A~C.
下面用矩阵的初等行变换来解方程组(2.22),其过程可与方程组(2.22)的消元过程一一对应.

由B4得到解(2.27)的回代过程,也可用矩阵的初等行变换来完成,即
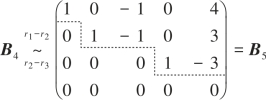
B5对应方程组为
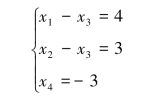
矩阵B4和B5都称为行阶梯形矩阵,其特点:可画出一条阶梯线,线的下方全为0;每个阶梯只有一行,台阶数即为非零行的行数,阶梯线的竖线(每段竖线的长度为一行)后面的第一个元素为非零元,即非零行的第一个非零元.
行阶梯形矩阵B5也称为行最简形矩阵.其特点:非零行的第一个非零元为1,且这些非零元所在列的其他元素全为0.
利用初等行变换,把一个矩阵化为行阶梯形矩阵和行最简形矩阵,是一种很重要的运算.由引例可知,要解线性方程组只需把增广矩阵化为行最简形矩阵.
由行最简形矩阵B5,即可写出方程组(2.22)的解(2.27);反之,由方程组的解(2.27)也可写出矩阵B5.由此可猜想到,一个矩阵的行最简形矩阵是唯一确定的(行阶梯形矩阵中非零行的行数也是唯一确定的).
对行最简形矩阵再施行初等列变换,可变成一种形状更简单的矩阵,称为标准形.例如:
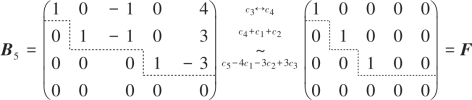
矩阵F称为矩阵B的标准形,其特点:F的左上角是一个单位矩阵,其余元素全为0.
对于m×n矩阵A,总可经过初等变换把它化为标准形:
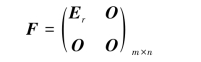
此标准形由m,n,r三个数完全确定,其中,r就是行阶梯形矩阵中非零行的行数.所有与A等价的矩阵组成一个集合,标准形F是这个集合中形状最简单的矩阵.
矩阵的初等变换是矩阵的一种最基本的运算,为探讨它的应用,需要研究它的性质.为此,先引进初等矩阵的知识.
