3.7.2　向量组生成的向量空间

3.7.2　向量组生成的向量空间

例3.7.4　已知向量组α1,α2,…,αs,且

证明V为向量空间.

证明　若

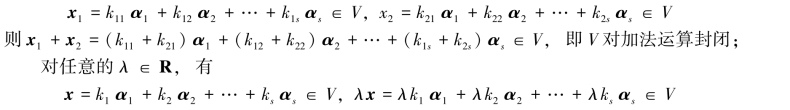
即V对于数乘运算封闭.所以V为向量空间.

由此得到的向量空间V,称为由α1,α2,…,αs生成的向量空间,记为L(α1,α2,…,αs).(https://www.daowen.com)

定理3.7.1　设V=L(α1,α2,…,αs),则V与α1,α2,…,αs等价.

证明　由L(α1,α2,…,αs)的定义可知,V中每个向量都可由α1,α2,…,αs线性表示,而α1,α2,…,αs∈V,α1,α2,…,αs可由V线性表示,所以V与α1,α2,…,αs等价.

定理3.7.2　两个等价的向量组生成的向量空间相同.

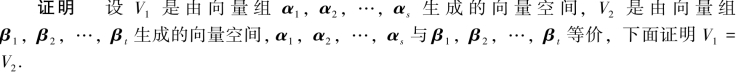
任取α∈V1,α可由α1,α2,…,αs线性表示,又α1,α2,…,αs与β1,β2,…,βt等价,所以α可由β1,β2,…,βt线性表示,即α∈V2,V1⊆V2.

同理可证V2⊆V1.综上,V1=V2.