1.1.2　三阶行列式的概念

1.1.2　三阶行列式的概念

定义1.1.2　称

为三阶行列式,其值等于a11a22a33+a12a23a31+a13a21a32-a11a23a32-a12a21a33-a13a22a31.

三阶行列式由三行、三列共九个元素组成,元素aij(1≤i,j≤3)的第一个下标i表示该元素在第i行,第二个元素j表示该元素在第j列.例如a32在第3行第2列.三阶行列式定义中共有六项,每项由来自不同行、不同列的三个元素的乘积组成,其中有三项前面带“+”号、三项前面带“-”号.图1.2可以帮助记忆,在主对角线及平行于主对角线的连线(用实线表示,即三条实线)上的三个元素的乘积前冠“+”号,在副对角线及平行于副对角线的连线(用虚线表示,即三条虚线)上的三个元素的乘积前冠“-”号.

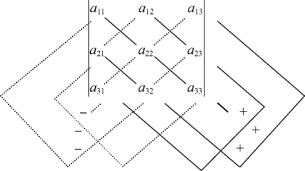
图1.2

例1.1.1　计算三阶行列式

解　D=2×6×(-1)+3×7×8+4×5×9-2×7×9-3×5×(-1)-4×6×8

=-12+168+180-126+15-192=33

例1.1.2　求解关于变量x的方程:

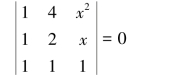
解　方程左端的三阶行列式D为

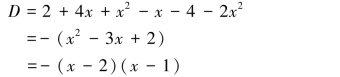
令D=0,即得-(x-2)(x-1)=0,于是,x=1或x=2.