5.4.3　二次型的标准形和规范形

5.4.3　二次型的标准形和规范形

在定性和定量地研究二次型时,需要对二次型的某些特征进行刻画,从而更加直观地把握二次型的性态.

定义5.4.4　称仅含有平方项的二次型

为标准的二次型,简称标准形.

从定义可知,标准形的矩阵为对角阵.如果标准形中的系数k1,k2,…,kn只在1,-1,0这三个数值中取值,会得到一个更加简洁的形式:

定义5.4.5　称式(5.11)为二次型的规范形.其中,p称为正惯性指数;负系数的个数r-p称为负惯性指数,r为二次型的秩.

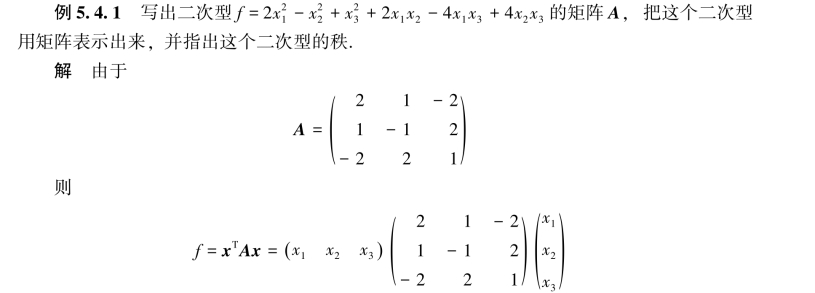
因为R(A)=3,所以这个二次型的秩为3.

定理5.4.1　在线性变换下,二次型仍变换为二次型.在可逆线性变换下,二次型的秩不变.

证明　设有从x1,x2,…,xn到y1,y2,…,yn的线性变换:

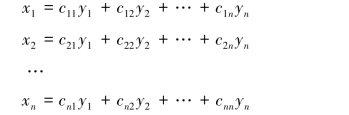
化二次型f=xTAx为标准形,cij为常数.

记矩阵C=(cij)n×n,即X=Cy,则f=xTAx=yTCTACy=yTBy,即f能化为关于y1,y2,…,yn的二次型,其中,B=CTAC.

当C为可逆矩阵时,有

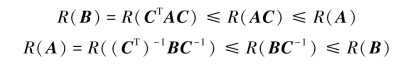
故R(A)=R(B).

可逆线性变换不改变二次型的秩,这一点非常重要.