过定点的曲线与曲面方程的建立

一、过定点的曲线与曲面方程的建立

例F2.1　天文学家通过观测数据确定一颗小行星绕太阳运行的轨道.具体做法:在轨道平面内建立以太阳为原点的直角坐标系,取天文单位测量单位(一个天文单位为地球到太阳的平均距离1.496×108 km)作为坐标单位.在5个不同的时间对小行星进行5次观测,得到轨道上的5个点的坐标分别为(5.764,0.648),(6.286,1.202),(6.759,1.823),(7.168,2.526)与(7.408,3.360).根据开普勒第一定律知小行星的运行轨道为一个椭圆,试建立该椭圆方程.

解　根据平面解析几何学,平面上的圆锥曲线:椭圆、双曲线、抛物线的一般方程为

该方程中有6个待定系数,但是,由于6个系数中必存在一个非零的,因此可以将方程两端同除以这个非零的系数.于是,只要5个方程就可以求解系数的值.

将在不同时间对小行星所进行的5次观测值,即轨道上5个点的坐标代入(1)并与式(1)一起构成以a1,a2,…,a6为未知变量的线性方程组:

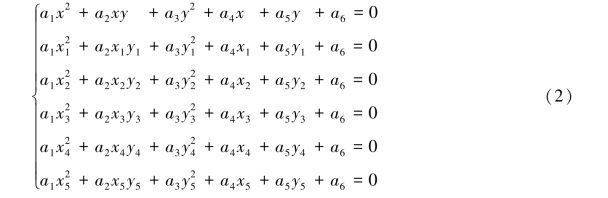
根据齐次线性方程组有非零解的充分必要条件,方程组(2)的系数行列式应该为0.

准备数据见附表2.

附表2　系数行列式中的数据

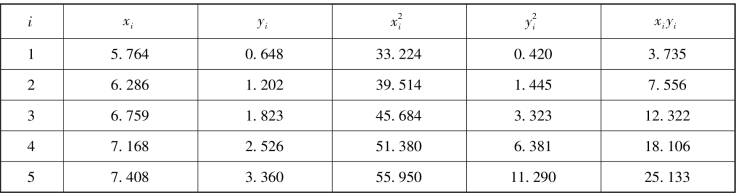
于是,小行星的运行轨道的椭圆方程为