5.1.2 特征值和特征向量的求解
2026年01月14日
5.1.2 特征值和特征向量的求解
方阵A(可被视为某个线性变换的矩阵)的特征值和特征向量的求法可以归纳为以下步骤:
(1)求出方阵A的特征方程f(λ)=det(A-λE)=0的全部根,它们就是A的特征值;
(2)将求得的特征值逐个代入齐次线性方程组:
![]()
求其非零解,在表述为通解时要注意非零常数的选取,得到属于每个特征值的全部特征向量.

解 A的特征多项式为
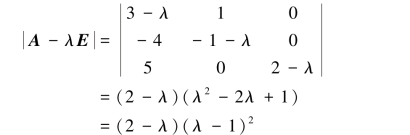
得A的特征值λ1=2,λ2=λ3=1.
当λ1=2时,解线性方程组(A-2E)x=0,由
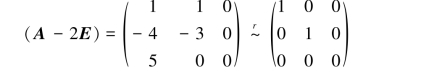
得基础解系为
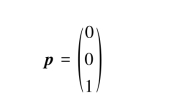
所以,kp1(k∈R,k≠0)是对应于λ1=2的全部特征向量.
当λ2=λ3=1时,解线性方程组(A-E)x=0,由
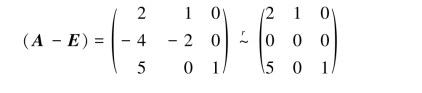 (https://www.daowen.com)
(https://www.daowen.com)
得基础解系为
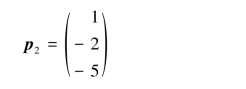
所以,tp2(t∈R,t≠0)是对应于λ2=λ3=1的全部特征向量.

得A的特征值λ1=-1,λ2=λ3=2.
当λ1=-1时,解线性方程组(A+E)x=0,由
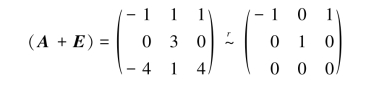
得基础解系为
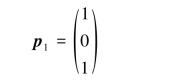
所以对应于λ1=-1的全部特征向量为kp1(k∈R,k≠0).
当λ2=λ3=2时,解线性方程组(A-2E)x=0,由
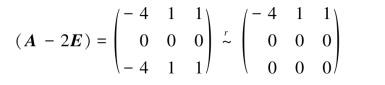
得基础解系为
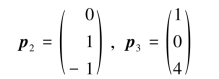
所以对应于λ2=λ3=2的全部特征向量为x=k2 p2+k3 p3(k2,k3∈R,且k2,k3不同时为0).
这两个例题都是特征方程有重根的情形.但是,例5.1.2的特征重根对应一个线性无关的特征向量,也就是A只有两个线性无关的特征向量;例5.1.3的特征重根对应两个线性无关的特征向量,也就是A有三个线性无关的特征向量,这个结论在矩阵对角化时十分重要.
