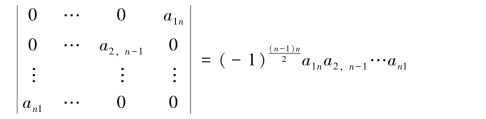1.3.2　几类特殊类型的行列式

1.3.2　几类特殊类型的行列式

主对角线以下(上)的元素都为零的行列式叫作上(下)三角形行列式.

例1.3.1　计算n阶上三角形行列式:

解　n阶上三角形行列式的特点是当i＞j时,aij=0.由于行列式展开式中的一般项为

在行列式第n行的元素中,除了ann可能不是零外,其他全部为零,因此,仅需要考虑jn=n的那些项.在第n-1行中,除了an-1,n-1和an-1,n可能不是零外,其他元素全部为零.因此,jn-1只有选取n-1和n这两种可能.由于jn=n,因而jn-1就不能选取n,只能选取n-1,即jn=n-1.这样逐步推下去,直到j1也只能选取1这一种可能,即j1=1.由此可以看出,在展开式中除了

这一项外,其余的项全部为零.而t(12…n)=0,故得

类似地,有下三角形行列式:

特殊情况:除主对角线元素以外的其他元素全为零的行列式称为对角形行列式,如

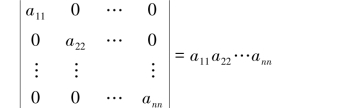
例1.3.2　计算n阶行列式:

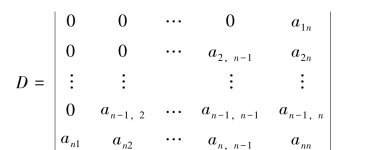
解　按n阶行列式定义:

行列式第1行的元素除了a1n可能不为零外其他元素全部为零,因此,仅需要考虑j1=n的那些项.在第2行中,除了a2,n-1和a2n可能不为零外其他元素全部为零,因此,j2只有选取n-1和n这两种可能.由于j1=n,因而j2就不能选取n,只能选取n-1,即j2=n-1.这样逐步推下去,直到jn也只能选取1这一种可能,即jn=1.由此可以看出,在展开式中除了

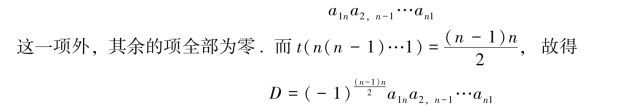
类似地,有

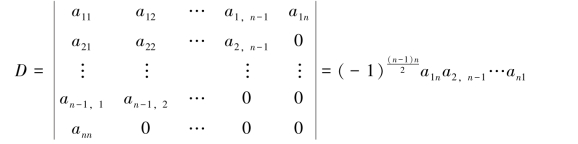
特殊情况: