2.3.1　矩阵逆的概念

2.3.1　矩阵逆的概念

设给定一个线性变换:

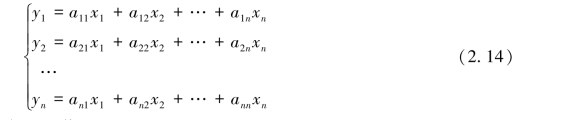
它的系数矩阵是一个n阶矩阵A,若记

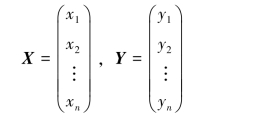
则线性变换(2.14)可记作

以A的伴随阵A*左乘上式两端,可得

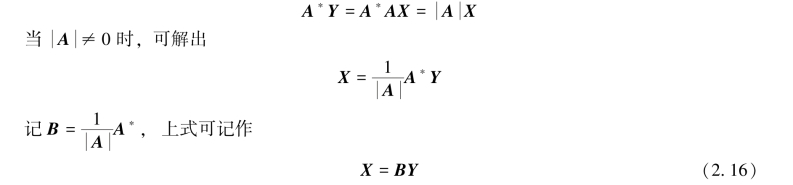
式(2.16)表示一个从Y到X的线性变换,称为线性变换(2.15)的逆变换.将式(2.16)代入式(2.15),可得

可见AB为恒等变换所对应的矩阵,故AB=E.将式(2.15)代入(2.16),可得

于是有BA=E.从而有

由此引入逆矩阵的定义.

定义2.3.1　对于n阶矩阵A,如果有一个n阶矩阵B,使

则称矩阵A是可逆的,并称B为A的逆矩阵,简称逆阵.

若矩阵A可逆,则A的逆阵是唯一的.事实上,假设B和C都是A的逆矩阵,即同时有

则

所以A的逆阵是唯一的.

A的逆阵记作A-1,即若AB=BA=E,则B=A-1.

因此,按逆矩阵的定义,可知A可逆,且有