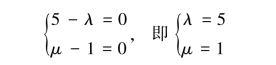2.6.2 秩的求法
故R(A)=2.
矩阵的最高阶非零子式可能不止一个.在例2.6.1中,A的9个2阶子式恰好都不等于零,因此A中任何一个二阶子式都是A的最高阶非零子式.
解 A是一个行阶梯形矩阵,其非零行有三行,即知A的所有四阶子式全为0.而以三个非零行的第一个非零元为对角元的三阶行列式
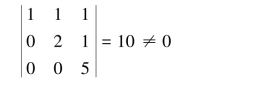
故R(A)=3.
由例2.6.2可知,对于一般的矩阵,当行数与列数较高时,按定义求秩是相当麻烦的.但由于阶梯形矩阵的秩等于非零行的行数,因此可利用初等变换把矩阵化为行阶梯形矩阵,但变换前后的两个矩阵的秩是否相等呢?下面的定理对此作出了肯定的回答.
定理2.6.1 若A~B,则R(A)=R(B).
证明 设R(A)=r,且A的某个r阶子式D≠0.
若p=2,则D1=D≠0;若p≠2,则D2也是B的r阶子式,由D1-kD2=D≠0可知,D1与D2不同时为0.总之,B中存在r阶非零子式D1或D2,故R(B)≥r.
至此,证明了若A经一系列初等行变换变成B,则R(A)≤R(B).又由于B也可经一系列初等行变换变成A,故也应有R(B)≤R(A).因此,R(A)=R(B).
经一次初等行变换矩阵的秩不变,即可知经有限次初等行变换矩阵的秩也不变.
设A经初等列变换变成B,则AT经初等行变换变成BT,从而有R(AT)=R(BT),又由于R(AT)=R(A),R(BT)=R(B),因此R(A)=R(B).
总之,若A经有限次初等变换变成B(即A~B),则R(A)=R(B),即初等变换不改变矩阵的秩.至此定理2.6.1证毕.
推论2.6.1 若存在可逆矩阵P,Q,使得PAQ=B,则R(A)=R(B).
定理2.6.1表明,要求矩阵的秩,只要把矩阵用初等行变换变成行阶梯形矩阵,则行阶梯形矩阵中非零行的行数即为该矩阵的秩.
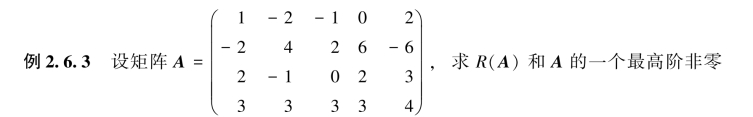
子式.
解 对矩阵A施行初等行变换,有
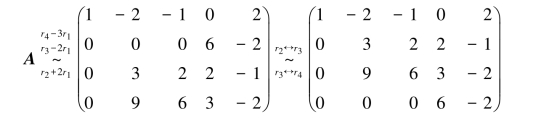
于是有R(B)=3,故B中必有3阶非零子式.B的3阶子式共有4个,在B的3阶子式中找一个非零子式,比在A中找非零子式要容易得多.由于B的前三行构成的子式为
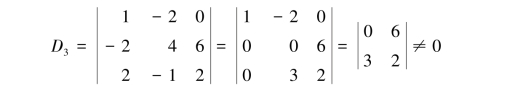
因此D3即为A的一个最高阶非零子式.
故R(A)=2,R(B)=3.
从矩阵B的行阶梯形矩阵可知,本例中的A与b所对应的线性方程组Ax=b是无解的,这是因为行阶梯形矩阵的第三行表示矛盾方程0=1.
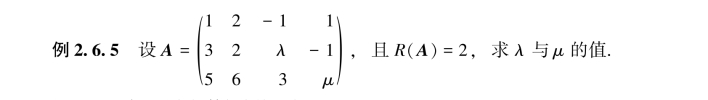
解 对矩阵A施行初等行变换,有
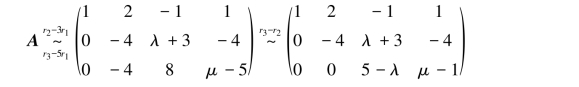
由于R(A)=2,故
