本章小结

本章主要介绍线性方程组的解的结构及其通解的求法.由n元齐次线性方程组Ax=0的解的性质可知,齐次线性方程组有无穷多解时,其通解可表示为x=c1ξ1+c2ξ2+…+cn-rξn-r,其中,r为系数矩阵A的秩R(A),ξ1,ξ2,…,ξn-r为齐次线性方程组的基础解系,即n-R(A)个线性无关的解向量,c1,c2,…,cn-r为任意实数.需注意的是基础解系不唯一,但其中所含解向量的个数唯一,等于R(S)=n-R(A).由n元非齐次线性方程组Ax=b的解的性质可知,当方程组有无穷多解时,其通解可表示为x=k1ξ1+k2ξ2+…+kn-rξn-r+η*,其中,c1ξ1+c2ξ2+…+cn-rξn-r为相应的齐次线性方程组的通解,η*是非齐次线性方程组Ax=b的一个解.这也是非齐次线性方程组的通解的结构.

具体的线性方程组的求解一般采用对系数矩阵或增广矩阵进行初等行变换化成行最简形矩阵的方法进行.抽象的方程组求解则利用解的性质.线性方程组求解是本章的重点内容.

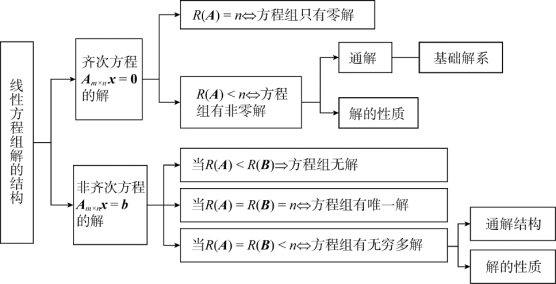
本章知识结构图如下: