延展阅读
线性空间和线性变换是现代数学的一个重要课题.
一、线性空间与Dürer魔方
所谓魔方又称幻方,是指由1~n2这n2个正整数按一定规则排列成的一个n行n列的正方形,且每行、每列与对角线上的n个元素之和都相等,n称为此魔方的阶.构造魔方是一个古老的数学游戏,最早起源于中国,在中国古代又叫“河图”“洛书”或“纵横图”.大约15世纪时,魔方传到了西方,魔方自古以来在亚、欧、美洲的不少国家都被作为驱邪避凶的吉祥物,至今还有人把它当作符咒用于某些迷信活动.13世纪时,中国南宋数学家杨辉在世界上首先开展了对魔方的系统研究,欧洲14世纪也开始了这方面的工作.现在,魔方仍是组合数学的研究课题之一.这里我们利用线性空间的概念来研究一种特殊的魔方——Dürer魔方.
1514年德国著名艺术家Albrecht Dürer(1471—1521)铸造了一枚铜币,铜币右上角的几何图形就是一个魔方,如图6.1所示.它的每行、每列、每条对角线上的数字之和是34;若把其按矩阵分块,每四个元素一块,其数字之和也是34,四个角上的数字相加仍等于34.这样的魔方就称为Dürer魔方.

图6.1
利用线性空间的思维方法可以研究Dürer魔方.下面的两个魔方分别称为0-魔方和1-魔方:

D中元素的线性组合构成新的魔方,因此D构成线性空间,称为Dürer魔方空间,简称D-空间.下面给出此空间的基和维数.
对0,1两个数字组合,可以构造和为1的所有魔方,称之为基本魔方,记为Pi,i=1,2,…,8.
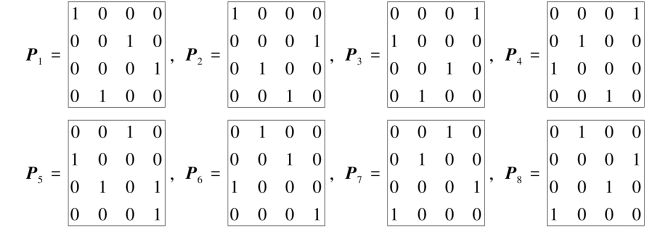
可以验证Pi,i=1,2,…,8线性相关,而P1,P2,…,P7是线性无关的,所以P1,P2,…,P7是D-空间的一组基,D中任何元素都可由P1,P2,…,P7的线性组合表示,且Dürer魔方空间的维数为7.(https://www.daowen.com)
利用线性方程组可以解出,Dürer魔方在此组基下的坐标为
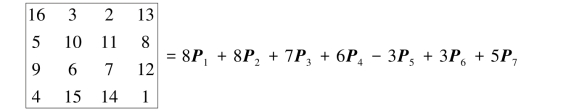
1967年Bostch证明了可以构造大量D的子空间.如果对各类空间中的元素赋予一定的含义,则可以在规定范围内进行信息传递,这也在密码学中有着广泛的应用.
二、线性空间与现代控制理论
2020年12月17日,嫦娥五号登月探测器顺利带着采集到的样品返回地球,意味着我国航天技术的一次重大跨越,为进一步认识月球提供重要支撑.空间飞行器是一个不稳定的中机体,在大气层时需要不断地使用计算机进行监控,这需要现代控制理论的支撑.从数学的角度看,工程中控制系统输入和输出的信号都是函数,这些函数的加法和数乘是控制系统的基本运算.现代控制理论的数学基础依赖于函数的线性空间,因此把n维线性空间推广到无穷维,对于控制系统的研究和设计是不可或缺的.一个控制信号在离散时间上被测量时,测量信号总体就可以构成双向无穷序列空间.嫦娥五号探测器的控制系统就是使用了各类传感器采集的离散数字信号,最终实现自主导航控制的.
三、线性变换与人工智能
人工智能(AI)是计算机科学或智能科技中设计研究、设计和应用智能机器的一个分支,是集心理认知、机器学习、情感识别、人机交互、数据保存及决策于一身的多学科技术.要把人工智能系统做得像人类,核心能力包括感知能力、运动控制能力、学习推理能力.对于感知能力的处理需要计算机能够对图像、声音等数据进行处理,而这些正需要线性代数中的线性变换.
在线性空间中,一个矩阵就对应一个线性变换,通过矩阵乘法实现.这些变换包括对于向量的旋转、缩放和映射.线性变换通过矩阵乘法对图像或语音数据进行增强,如将图像沿着某个方向平移、对图像进行旋转或缩放等以产生新的图像.例如在R2中的任意线性变换都可通过齐次坐标(R2中的点对应于R3中的坐标)乘以3×3矩阵实现.如
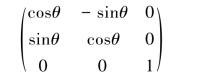
表示绕原点逆时针旋转角度θ,而
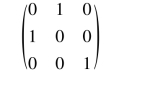
则表示关于y=x的对称变换.
