同步习题
一、填空题.(每题4分,共20分)
1.设齐次线性方程组Am×nx=0的系数矩阵的秩为r,已知r＜n,则其基础解系含解向量的个数为________.
2.方程组x1+x2+x3+x4+x5=0的基础解系为________.
3.(2019,数一)设A=(α1,α2,α3)为3阶矩阵,若α1,α2线性无关,且α3=-α1+2α2,则线性方程组Ax=0的通解为________.
是导出组Ax=0的解向量的个数为( ).
(A)4 (B)3 (C)2 (D)1
2.设A为n阶方阵,R(A)=n-3,且α1,α2,α3是Ax=0的三个线性无关的解向量,则Ax=0的基础解系可表示成( ).
(A)α1,α2,α3的一个等价向量组 (B)α1,α2,α3的一个等秩向量组
(C)α1,α2+α1,α1+α2+α3 (D)α1-α2,α2-α3,α3-α1
3.(2011,数一)设A=(α1,α2,α3,α4)是4阶矩阵,A*为A的伴随矩阵,若(1,0,1,0)T是方程组Ax=0的一个基础解系,则A*x=0基础解系可为( ).
图4.2
三、(5分)求齐次线性方程组
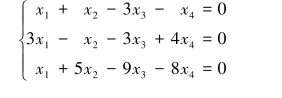
的基础解系与通解.
四、(6分)设四元齐次线性方程组分别为
求:(1)方程组Ⅰ与Ⅱ的基础解系;(2)Ⅰ与Ⅱ的公共解.
五、(5分)求非齐次线性方程组的一个解及对应的齐次线性方程组的基础解系:
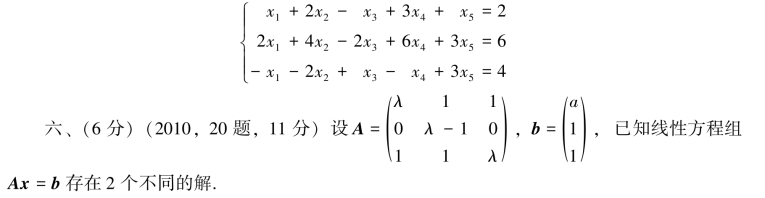
(1)求λ,a;(2)求方程组Ax=b通解.
七、(5分)设三元非齐次线性方程组的系数矩阵A的秩为1,已知η1,η2,η3是它的三个解向量,且η1+η2=(1,2,3)T,η2+η3=(2,-1,1)T,η3+η1=(0,2,0)T,求该非齐次方程组的通解.
八、(6分)设α1,α2,α3是齐次线性方程组Ax=0的一个基础解系,试证明:α1+α2,α1+α3,α1也是该方程组的一个基础解系.
九、(6分)λ取何值时,线性方程组:
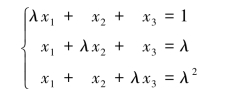
(1)有唯一解;(2)无解;(3)有无穷多个解,并在有无穷多解时,求出通解.
十、(5分)设A为n阶矩阵(n≥2),A*为A的伴随矩阵,证明:
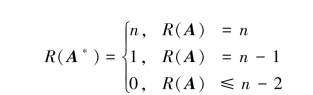
十一、(6分)设η*是非齐次线性方程组Ax=b的一个解,而ξ1,ξ2,…,ξn-r是对应的齐次线性方程组Ax=0的一个基础解系,证明:
(1)η*,ξ1,ξ2,…,ξn-r线性无关;
(2)η*,ξ1+η*,ξ2+η*,…,ξn-r+η*线性无关.
十二、(5分)设η1,η2,…,ηs是非齐次线性方程组Ax=b的s个解,k1,k2,…,ks为实数,满足k1+k2+…+ks=1.证明:
也是该非齐次线性方程组的解.
十三、(5分)设非齐次线性方程组Ax=b的系数矩阵的秩为r,η1,η2,…,ηn-r+1是它的n-r+1个线性无关的解,试证明它的任一解可表示为
其中,k1+k2+…+kn-r+1=1.