6.1.1　线性空间的概念和性质

6.1.1　线性空间的概念和性质

1.线性空间的概念

定义6.1.1　设V是一个非空集合,R是实数域.如果对于任意两个元素α,β∈V,总有唯一的一个元素γ∈V与之对应,称γ为α与β的和,记作γ=α+β,称此运算为加法运算,又对于任一常数k∈R与任一元素α∈V,总有唯一的元素δ∈V与之对应,称δ为k与α的积,记作δ=kα,称此运算为数乘运算;并且这两种运算满足以下八条运算规律:

(1)对于任意α,β∈V,有α+β=β+α;

(2)对于任意α,β,γ∈V,有(α+β)+γ=α+(β+γ);

(3)V中存在零元素0,对于任何α∈V都有α+0=α;

(4)对于任一α∈V,都有α的负元素β∈V,使得α+β=0;

(5)对于实数域R的数1,有1α=α;

(6)对于任意k,l∈R和α∈V,有k(lα)=(kl)α;

(7)对于任意k,l∈R和α∈V,(k+l)α=kα+lα;

(8)对于任意k∈R和α,β∈V,k(α+β)=kα+kβ.那么,称V为实数域R上的线性空间(或向量空间),V中的元素称为(实)向量.

满足上面八条规律的加法和数乘运算称为线性运算.所以,定义了线性运算的集合就是线性空间.定义中一个重要的部分是加法运算与乘数运算的封闭性,与前面向量空间的定义类似,封闭性是必要的.另外,如果给定一个集合V,并在其上定义了满足封闭性的加法和数乘运算,则必须检验八条运算规律是否满足.下面用例子进行说明.

定义6.1.2　实数域R上的m×n阶矩阵所构成的集合,按通常矩阵的加法和数与矩阵的乘法运算,构成R上的一个线性空间,记为Rm×n.n个有序实数组成的数组的全体

对于通常的有序数组的加法以及如下定义的数乘运算:

不构成R上的线性空间.

事实上,虽然Sn对所定义的运算封闭,但是由于1°x=0≠x,即不满足运算规律(5),所以所定义的运算不是线性运算,故Sn不是线性空间.

但是,Sn按通常的有序数组的加法和数乘运算就构成线性空间,即向量空间Rn.

一般来讲,同一个集合可以定义不同的线性运算构成不同的线性空间;如果定义的运算不是线性运算就不构成线性空间.所以,线性运算是线性空间的本质,而其中的元素是什么并不重要.

例6.1.1　试证明:实数域R上次数不超过n的多项式的全体为P[x]n,即

对于通常的多项式的加法与数乘多项式运算构成线性空间,而实数域R上次数为n的多项式的全体为Q[x]n,即

对于通常的多项式加法和数乘多项式运算不构成R上的线性空间.

证明　由于

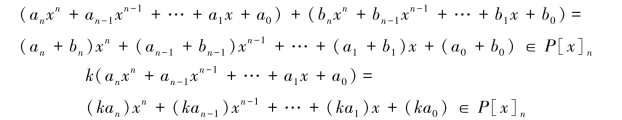
即P[x]n对通常的多项式的加法及数乘多项式运算封闭,而且满足八条运算规律,故次数不超过n的多项式的全体P[x]n构成R上的线性空间.

但是,由于0(anxn+an-1xn-1+…+a1x+a0)=0∉Q[x]n,因此Q[x]n,对数乘多项式运算不封闭.因而Q[x]n,不构成线性空间.

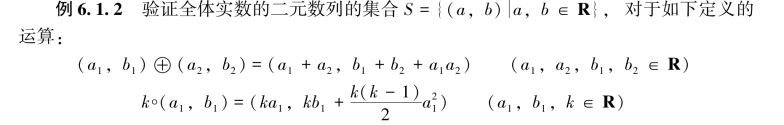
构成R上的线性空间.

证明　显然,全体实数的二元数列的集合S对于所定义的运算是封闭的,且满足下面八条运算规律:

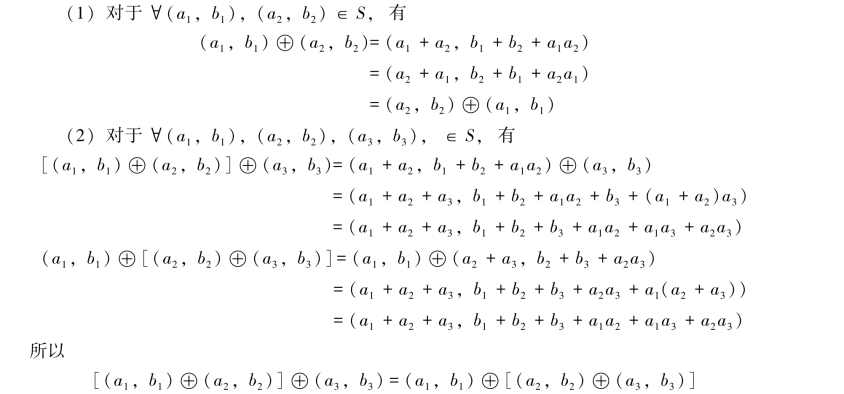
(3)S中存在零元素(0,0);对于任一(a,b)∈S,有

(4)对于S中任意元素(a,b)都有负元(-a,a2-b)∈S,使得

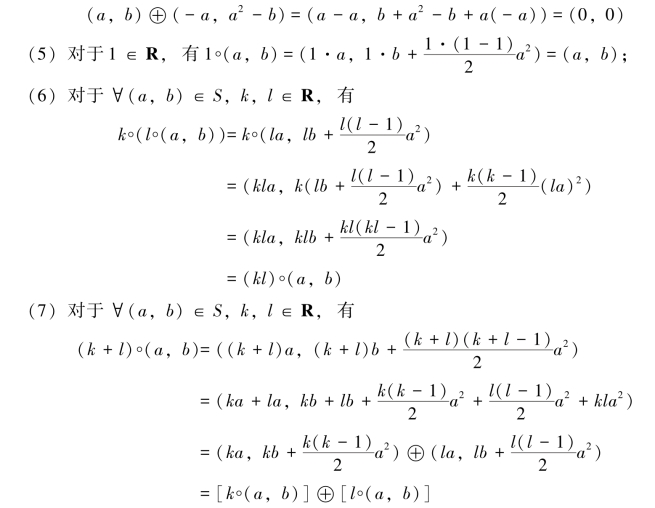
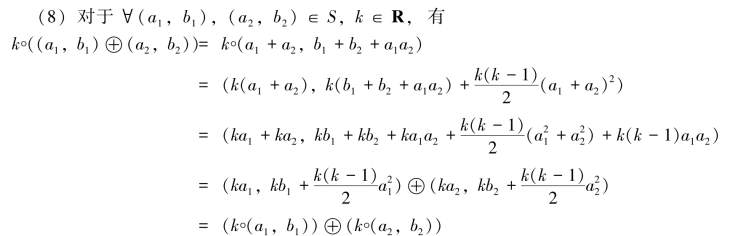
因此,S对于所给运算构成实数域R上的线性空间.

2.线性空间的性质

性质6.1.1　线性空间V中的零元素是唯一的.性质6.1.2　线性空间V中的负元素是唯一的,每个元素α的负元素通常记作-α.

由定义,本章中定义的线性空间是第4章向量空间概念的拓展,线性空间中的元素不仅仅是向量,两种运算也不局限于向量的加法和数乘.向量空间是线性空间的特例,如果把线性空间中元素广义地称为向量,则线性空间也可称为向量空间.前面定义过的线性组合、线性相关与线性无关等概念和某些性质可以平行推移到一般的线性空间中.