1.7.1 非齐次线性方程组
2026年01月14日
1.7.1 非齐次线性方程组
与1.1.1中二元线性方程组类似,可以用n阶行列式求解n元线性方程组,为此引进克拉默法则.
定理1.7.1 如果含有n个方程的n元线性方程组
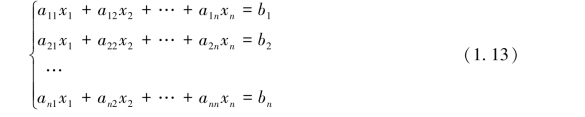
的系数组成的行列式
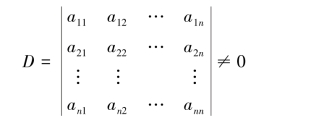
那么线性方程组(1.13)有唯一解:
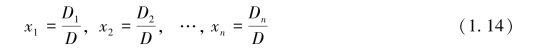
其中,Di(i=1,2,…,n)的构成如下:(https://www.daowen.com)
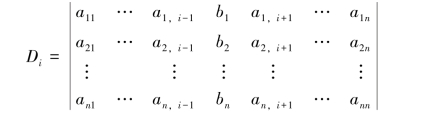

定理1.7.1通常称为克拉默(Cramer)法则,证明详见2.4节.由克拉默法则可知,如果线性方程组(1.13)没有唯一解(即无解或有两组及以上的解),则系数行列式一定为零,即D=0.
例1.7.1 用克拉默法则解下面的线性方程组:

方程组中后两个方程相互矛盾,所以,方程组无解.
几何解释:每个三元一次方程都是一个平面,可以验证,第一、第二个方程的交线的方向向量为(-1,0,1)T与第三个方程的法向量(1,0,1)T垂直,即交线与第三个平面平行,所以,三个平面没有交点,亦即方程组无解.
