5.2.1 相似矩阵的概念和性质
定义5.2.1 设A,B都是n阶方阵,若有可逆方阵P,使
![]()
则称B是A的相似矩阵,或说矩阵A与B相似.对A进行的运算P-1AP称为对A进行相似变换,可逆方阵P称为把A变成B的相似变换矩阵.
相似变换使矩阵A和一个比较简单的矩阵B建立了关系式P-1AP=B,可以使问题的求解更加简单.
相似关系是同阶方阵之间的一种关系,具有下列性质:
(1)自反性:A与A相似.因为取单位阵E,有E-1AE=A成立.
(2)对称性:若B与A相似,则A与B相似,因为式(5.3)两端左乘P,右乘P-1,有PBP-1=A成立.
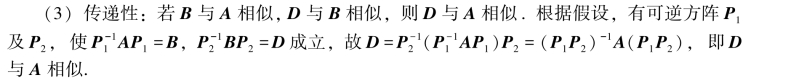
定理5.2.1 若n阶方阵A与B相似,则A与B的特征多项式相同,从而A与B的特征值亦相同,而且det A=det B.
证明 因为A与B相似,即有可逆矩阵P,使P-1AP=B,故
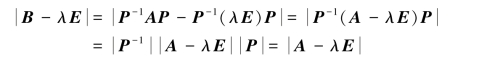
即A与B的特征值亦相同,且有

解 根据特征多项式的定义,有
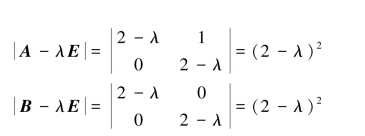
所以A与B的特征多项式相同.
假设A与B相似,即存在可逆矩阵P,使P-1AP=B,即
 (https://www.daowen.com)
(https://www.daowen.com)
因为相似变换不改变矩阵的特征值,所以可以通过相似变换,把A变成最简单的形式来解决问题.最简单的形式就是对角矩阵.
推论5.2.2 若n阶方阵A与对角阵

证明 因λ1,λ2,…,λn是对角阵Λ=diag(λ1,λ2,…,λn)的n个特征值,由定理5.2.1知,若n阶方阵A与B相似,则A与B的特征值相同,因此,λ1,λ2,…,λn是A的n个特征值.

由矩阵的相似性,可以简化矩阵多项式的计算.
如果B=P-1AP,φ(x)是一个多项式,则有φ(B)=P-1φ(A)P.如果矩阵B相似于一个比较简单的矩阵A,φ(A)是容易计算的,就可以通过φ(B)=P-1φ(A)P来简单地计算φ(B).
特别地,当φ(x)就是特征多项式时,有结论:φ(A)=f(A)=O.习惯上把特征多项式记作f.
我们只在A与对角矩阵相似的情况下,证明这个重要结论.


例5.2.3 已知3阶方阵A的特征值为1,-1,2,求A2+3A-2E的特征值.
解 记φ(A)=A2+3A-2E,即φ(λ)=λ2+3λ-2,有φ(1)=12+3×1-2=2,φ(-1)=(-1)2+3×(-1)-2=-4,φ(2)=22+3×2-2=8.
由此可得多项式矩阵A2+3A-2E的特征值为2,-4,8.
例5.2.4 设方阵A满足A2-3A+2E=O,证明A的特征值只能取1或2.
证明 设λ是方阵A的特征值,记φ(λ)=λ2-3λ+2,则φ(λ)是A2-3A+2E的特征值;
由A2-3A+2E=O,得φ(λ)=λ2-3λ+2=0,即φ(λ)=λ2-3λ+2=(λ-1)(λ-2)=0,所以,A的特征值只能取1或2.
