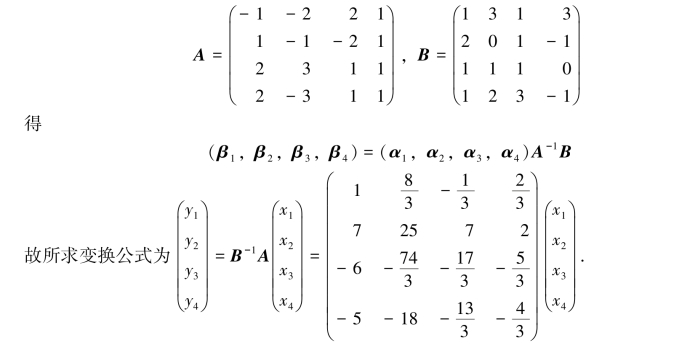§6.2 基变换与坐标变换
很多应用问题可以通过一个坐标系转化为另一坐标系而得到简化.线性空间有不同的基,并且同一个元素在不同基下的坐标是不同的,如何进行基与基之间、同一元素在不同基下的坐标直接变换是本节要讨论的问题.
定义6.2.1 设α1,α2,…,αn和β1,β2,…,βn是n维线性空间Vn中的两个基,那么它们之间可以互相表示,设
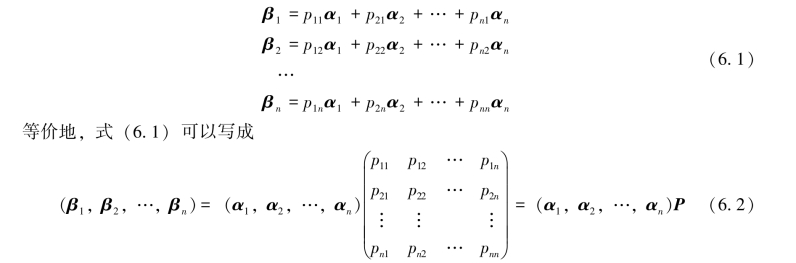
称式(6.1)或式(6.2)为基变换公式,称矩阵P为由基α1,α2,…,αn到基β1,β2,…,βn的过渡矩阵.
过渡矩阵刻画了同一个有限维线性空间的不同基之间的关系,由基的线性无关性可知过渡矩阵是非奇异的.
定理6.2.1 设n维线性空间Vn中的元素ξ在基α1,α2,…,αn和基β1,β2,…,βn下的坐标分别为(x1,x2,…,xn)T和(y1,y2,…,yn)T,如果两个基满足关系式(6.2),则有坐标变换公式:
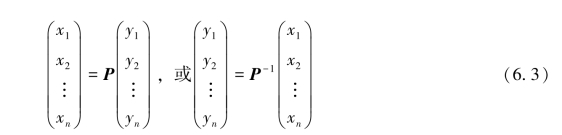
证明 由ξ在基α1,α2,…,αn和基β1,β2,…,βn下的坐标分别为(x1,x2,…,xn)T和(y1,y2,…,yn)T以及式(6.2),有
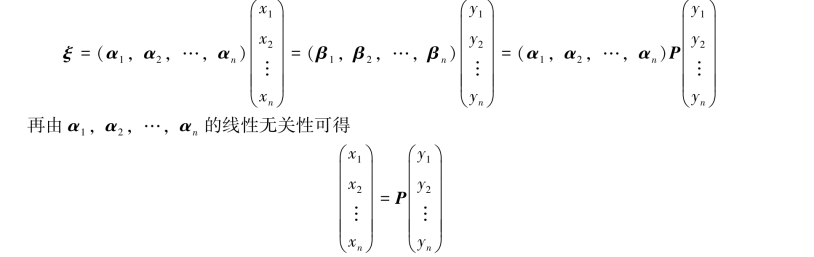
注意:若任一元素的两种坐标满足坐标变换公式(6.3),则两个基满足基变换公式(6.2),即这个定理的逆命题也成立.
例6.2.1 设向量空间R3的两个基为
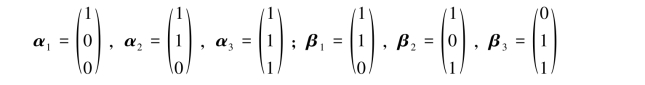
求由基α1,α2,α3到基β1,β2,β3的过渡矩阵.
解 设由基α1,α2,α3到基β1,β2,β3的过渡矩阵为C,则由式(6.2)可得
即
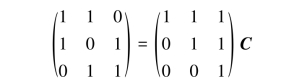
于是得由基α1,α2,α3到基β1,β2,β3的过渡矩阵为
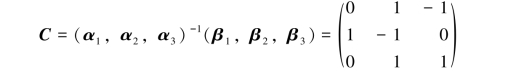
例6.2.2 在P[x]3中取两个基
(1)α1=-x3-2x2+2x+1,α2=x3-x2-2x+1,
α3=2x3+3x2+x+1,α4=2x3-3x2+x+1;
(2)β1=x3+2x2+x+1,β2=3x3+x+2,
β3=x3+x2+x+3,β4=3x3-x2-1.
求坐标变换公式.
解 取P[x]3中基x3,x2,x,1.因为
(α1,α2,α3,α4)=(x3,x2,x,1)A,(β1,β2,β3,β4)=(x3,x2,x,1)B
其中
