1.1.2 复数的表示
我们通常称z = x+iy为复数z的代数形式.除此之外,复数z还有多种表示形式,下面介绍复数的几种表示方法.
由于复数z =x+iy由一个有序实数对(x,y)唯一确定,在取定平面直角坐标系xOy时,实数对(x,y)可视为平面直角坐标系中的两个坐标组成的序对,这就建立了复数z与平面上的点的一一对应关系,于是对于任意一个复数z =x+iy,都对应于平面上的一点P(x,y),故可用实数对形式(x,y)表示.
由于所有实数与横坐标轴上的点一一对应,故我们称横坐标轴为实轴;同样地所有的纯虚数与除原点外的纵坐标轴上的点一一对应,故我们称纵坐标轴为虚轴.相对应于横,纵坐标所在的平面,我们把实轴,虚轴所在的平面称为复平面,或根据表示复数的字母z,w,··· ,称为z平面,w平面,···.显然,当y /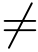
0 时,复数z 与
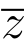关于实轴对称.
对于任意一个复数z都与平面上的点(x,y)对应,所以复数z也可以原点为起点,P(x,y)为终点的向量
对应,即复数z可用向量表示,如(图1-1).
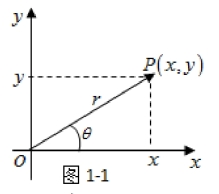
此时x和y分别是向量
在实轴和虚轴上的投影.向量
的长度
称为复数z =x+iy的模或绝对值,记作
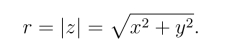
当z /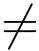
0时，以x轴的正方向为始边,向量
为终边的夹角θ称为复数z的辐角,记作Argz = θ.我们知道,以x轴的正方向为始边,
为终边的角有无限个,它们之间可以相差2π的整数倍,所以Argz有无穷多个值,即若θ1是复数z的任意一个辐角,则
在复数z 的全部辐角中,我们把满足-π ＜θ0 ≤π 的辐角θ0 称为Argz的主值,记作θ0 =arg z.
因此，对于任意非零复数z,
Argz =arg z+2kπ,k为任意整数.
当z = x+iy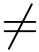 
0 时，幅角的主值可根据反正切
的主值
确定：
注：当z =0时，辐角无意义.
例1 求Arg(1+i)及
解 Arg(1+i)=arg(1+i)+2kπ =
k为整数;
为整数.
设r,θ分别为非零复数z = x+iy的模和辐角，由直角坐标与极坐标的关系：
x=r cos θ,y =r sin θ,
可把复数z表示成下面形式:
z =r(cos θ+i sin θ),
称为复数z的三角形式.
利用欧拉(Euler)公式：eiθ =cos θ+i sin θ,又可以得到
z =reiθ,
称为复数z的指数形式.
复数的各种表示法可以相互转换,以适应讨论不同问题时的需要.
例2 将下列复数化为三角形式与指数形式.
(1)z =-3i;(2)z =-1-i;(3)z =
解 (1)显然,
因此z的三角形式为
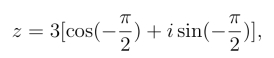
z的指数形式为
(2)由
知,z 的三角形式为
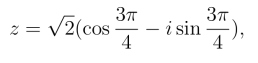
z的指数形式为
(3)易见r =1,由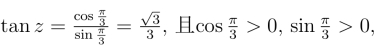
所以
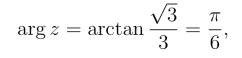
故z的三角形式为
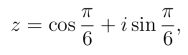
z的指数形式为
