习题五
1.下列函数有些什么奇点？如果是极点,指出它的级：
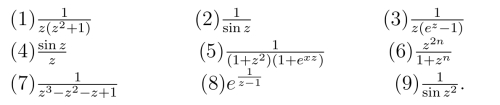
2.求证：如果z0是f(z)的级零点,则z0是f′(z)的m-1级零点.
3.设z0是函数f(z)的m级极点,又是g(z)的n级极点,试问下列函数在z0处具有何种性质？
4.函数f(z)=
在z =1处有一个2级极点; 这个函数又有下列洛朗展式
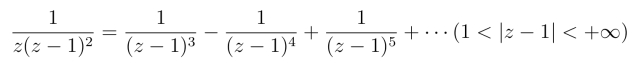
于是就说“z =1又是f(z)的本性奇点”,这个说法对吗？
5.下列函数在扩充复平面内有些什么类型的奇点？如果是极点,指出它的级.
6.求下列函数f(z)在有限奇点处的留数
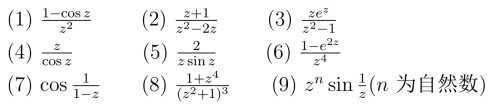
7.利用留数计算下列沿正向圆周的积分.
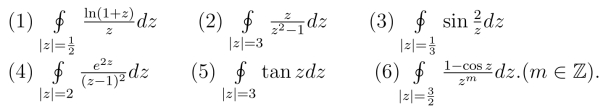
8.求Res[f(z),∞]的值,如果
9.计算下列各积分,C为正向圆周.
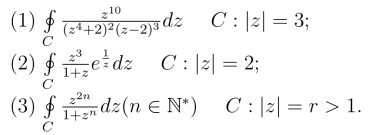
10.设P(z)与Q(z)是多项式,其中Q(z)的次数至少比P(z)的次数高两次.证明P(z)/Q(z)在有限奇点的留数的和等于零.
11.若函数φ(z)在点z0解析且φ′(z0)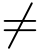 
0,又f(ξ) 在ξ = φ(z0)有留数为A的简单极点,求Res{f[φ(z)],z0}.
12.计算
的值.
13.计算积分
的值.
14.计算拉普拉斯积分
15.利用留数计算下列积分
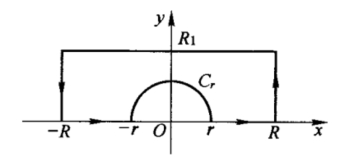
16.试用下图中的积分路线,求例6中的积分
17.利用公式(5.4.1)计算下列积分
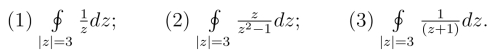
18.求方程z7-5z4+z2-2=0在|z|＜1内根的个数.
19.设φ(z)在圆周C :|z|=1上及其内部解析,且在C上|φ(z)|＜1,证明在C 内只有一个点z0使φ(z0)=z0
20.证明当|a|＞e时,方程ez-azn =0在单位圆周|z|=1内有n个根.
21.试证方程z5-z+3的所有根都在圆环1 ＜|z|＜2 内.
22.下列函数有些什么奇点？如果是极点,指出它的级.
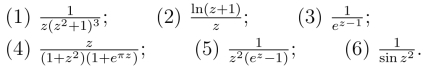
23.求下列函数在有限奇点处的留数.
24.求Res[f(z),∞]的值,若
25.求函数f(z)=
在它所有有限奇点处的留数之和.
26.利用留数计算下列积分.
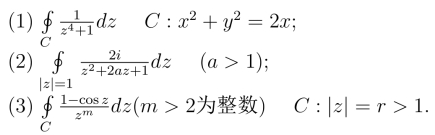
27.计算下列各积分,C为正向圆周.
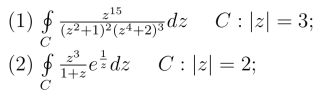
28.计算积分
其中C是圆环域1 ＜|z|＜3的正向边界.
29.计算积分
30.利用留数计算下列定积分.
31.计算积分
并由此证明
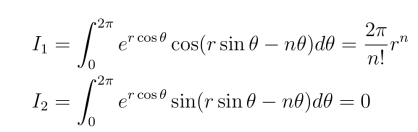
32.设函数f(z)与g(z)均在点心z0 = a解析,且a为它们的n级零点,试证a为
的可去奇点,且有
33.设函数f(z)在正向简单闭曲线C上解析,在C 的内部D除去有限个点zk(k = 1,2,··· ,m)外处处解析,如果对每个zk都有
试证
34.设函数f(z)在正向简单闭曲线C的外部D内解析,在C上也解析,并且
=A(A为常数),试证
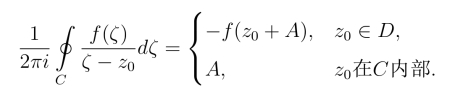
35.设函数f(z)在简单闭曲线C上及其内部D解析,如果f(z) 在D内点z0处有n级零点,而在D及C上无其他零点,试证对C的正向有
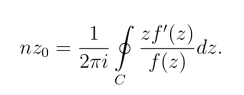
36.设函数f(z)在简单闭曲线C上及其内部D除在D内有m级极点z0外处处解析,且在C 上及D内无零点,试证对C的正向有
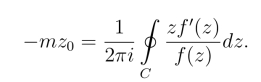
37.若f(z)在分段光滑闭曲线C上及其所围区域内除点z = a外解析,且a是f(z)的n级极点,求证: 当(z-a)nf(z)=g(z) 时,
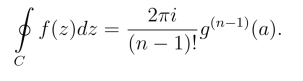
38.设φ(z)在C : |z| = l上及其内部解析,且在C上|φ(z)| ＜1.证明在C内只有一个点z0使φ(z0)=z0.
39.证明方程z7-z3+12=0的根都在圆环域1 ≤|z|≤2 内.