2.1.2 复变函数的极限与连续性
复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.
定义3 设函数w = f(z)在点z0的去心邻域:0 <|z - z0| <ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε >0,总存在一个实数δ >0(δ <ρ),当0 <|z-z0|<δ 时,有
|f(z)-A|<ε,
我们称A为f(z)当z趋于z0时的极限,记为
![]()
复变函数极限的几何意义与一元实函数类似,即当动点z进入z0的充分小的δ去心邻域时,它的象点f(z)就会落入A 的一个给定的ε邻域内.值得注意的是,这里的邻域是圆域,且z →z0,意味着点z在邻域内趋于z0 的方向是任意的.
特别地,我们也给出复变函数的极限为无穷大的定义.
定义4 设函数w = f(z)在点z0的去心邻域: 0 <|z-z0| <ρ内有定义.如果对于任意正数M,相应地存在δ >0(δ <ρ),使得当0 <|z-z0| <δ 时,有|f(z)|>M,我们称当z趋于z0 时,f(z) 的极限为无穷大,记为
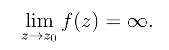
我们已经知道,给出一个复变函数w = f(z)可以用两个二元实变函数u = u(x,y)和v = v(x,y)表出,因此求复变函数w = f(z) = u(x,y) +iv(x,y)的极限问题可以转化为求两个二元实变函数u = u(x,y)和v =v(x,y)的极限问题.关于极限的计算,我们有下面两个定理.
定理1 设w =f(z)=u(x,y)+iv(x,y),A=u0+iv0,z0 =x0+iy0,则
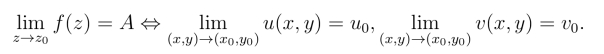
证明 由不等式
|u(x,y)-u0|≤|f(z)-A|≤|u(x,y)-u0|+|v(x,y)-v0|
及
|v(x,y)-v0|≤|f(z)-A|≤|u(x,y)-u0|+|v(x,y)-v0|
可以导出定理的结论.定理2 设复变函数f(z)与g(z)当z →z0时的极限分别为A 和B,即
![]()
则
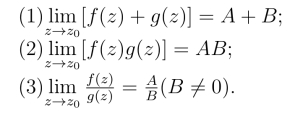 (https://www.daowen.com)
(https://www.daowen.com)
利用复变函数的极限的定义可证定理2,请读者自行证明.
例4 试证: 函数f(z)= ![]() 当z →0时的极限不存在.
当z →0时的极限不存在.
解 令z =x+iy,则
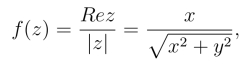
由此得u(x,y)=![]() ,v(x,y)=0.选取z →0的路径为y =kx,则有
,v(x,y)=0.选取z →0的路径为y =kx,则有
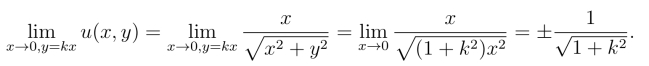
显然,当k变化时,极限值也会不同,所以![]() 0,根据定理1,
0,根据定理1,![]() 不存在.
不存在.
定义5 设w = f(z)在点z0的某一邻域: |z - z0| <δ内有定义,如果![]() 则称w = f(z)在点z0处连续.如果w = f(z)在区域D内每一点处都连续,则称w =f(z)在D 内连续.
则称w = f(z)在点z0处连续.如果w = f(z)在区域D内每一点处都连续,则称w =f(z)在D 内连续.
由定义5及定理1,易得下面的定理.
定理3 函数w = f(z) = u(x,y)+iv(x,y)在点z0 = x0+iy0处连续的充要条件是实部函数u(x,y) 与虚部函数v(x,y) 都在点(x0,y0) 处连续.
与高等数学中实变函数的连续函数的和、差、积、商(这时假设分母不为零)的定理以及连续函数的复合函数的定理类似,我们同样可以得到对应的复变函数的定理.
定理4 (1)若函数f(z)和g(z)都在点z0处连续,则f(z)±g(z),f(z)g(z)及![]() 均在点z0 处连续;
均在点z0 处连续;
(2) 若函数h = g(z) 在点z0处连续,函数w = f(h)在点h0 = g(z0) 处连续,则复合函数w =f(g(z))在点z0处连续.
在高等数学中,若函数f(z)在有界闭区域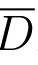 上连续,则可取到最大值和最小值.类似地,在复变函数中有相同的结论.
上连续,则可取到最大值和最小值.类似地,在复变函数中有相同的结论.
定理5 如果w =f(z)在有界闭区域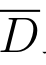 上连续,则f(z)在
上连续,则f(z)在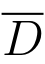 上可取到它的最大模和最小模,即存在z1,z2 ∈
上可取到它的最大模和最小模,即存在z1,z2 ∈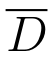 ,使得对于任意的z ∈
,使得对于任意的z ∈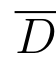 ,都有|f(z1)| ≥|f(z)|,|f(z2)|≤|f(z)|.
,都有|f(z1)| ≥|f(z)|,|f(z2)|≤|f(z)|.
由定理5,以下推论自然成立.
推论 如果w =f(z)在有界闭区域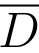 上连续,则w =f(z)在D上有界,即存在一个正数M使得对于任意的z ∈
上连续,则w =f(z)在D上有界,即存在一个正数M使得对于任意的z ∈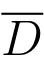 ,|f(z)|≤M.
,|f(z)|≤M.
还应指出,函数w =f(z)在曲线C上点z0处连续是指:
![]()
在闭曲线或包含曲线端点在内的曲线段C上连续的函数w = f(z)在曲线上是有界的,即存在一个正数M使得对于任意的z ∈C,|f(z)|≤M.
