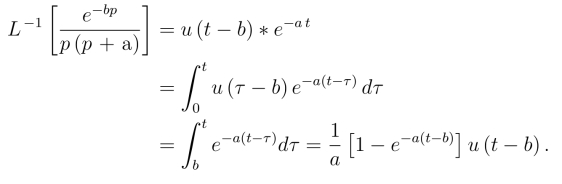8.4.3　卷积定理

8.4.3　卷积定理

定理1 设f1(t)与f2(t)满足拉氏变换存在定理中的条件,且L[f1(t)] =F1(p),L[f2(t)]=F2(p),则f1(t) *f2(t) 的拉氏变换存在,且

或

证明 容易证明f1(t) *f2(t)满足拉氏变换存在定理中的条件.

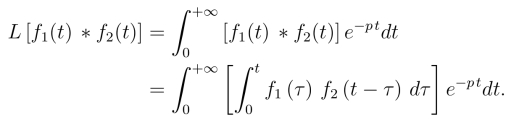
由上式可知,积分区域为图8-3所示的阴影部分.由于二重积分绝对可积,故可交换积分次序,即

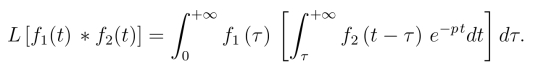
令u=t-τ,则

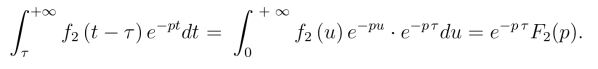
于是得到

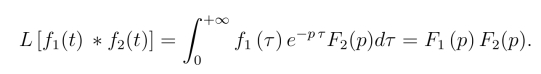
不难推证,若fk(t)(k =1,2,··· ,n)满足拉氏变换存在定理中的条件,且

(https://www.daowen.com)

则

例2 若F(s)= 求f(t).

解 因为

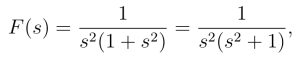
取

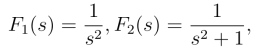
于是f1(t)=t,f2(t)=sin t.根据卷积定理得

例3 求L-1

解 因为

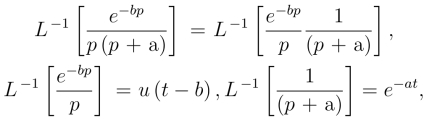
所以