6.2　分式线性映射

分式线性映射是很重要的一类映射,在实际中有广泛的应用.所谓分式线性映射是指

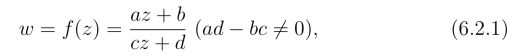
其中a,b,c,d为复常数.

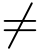由于f′(z) = 为了保证映射的保角性,应要求ad-bc 0,否则将有f′(z)=0,从而f(z)≡常数,它将整个z平面映射成w平面上的一个点.

用cz+d乘式（6.2.1)的两边,得

对每一个固定的w,上式关于z是线性的,而对每一个固定的z,它关于w 也是线性的.这样,上式是双线性的.因此,分式线性映射又称双线性映射.分式线性映射是德国数学家默比乌斯(M¨obius,1790～1868)首先研究的,所以也称默比乌斯映射.

由式(6.2.1)可解得z的w表达式,即逆映射：

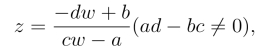
所以分式线性映射的逆映射也是一个分式线性映射.

容易证明,两个分式线性映射的复合仍是一个分式线性映射.