2.4.4　三角函数与双曲函数

2.4.4　三角函数与双曲函数

由复变函数的指数形式和三角形式可知,当x=0时,

eiy =cos y+i sin y,e-iy =cos y-i sin y.

将以上两式相加与相减,分别得到

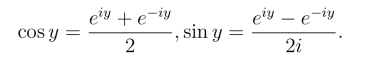
现在把实变量y推广到复变量z的情况,我们有如下定义：

定义4 对任意的复数z,定义正弦函数与余弦函数分别为

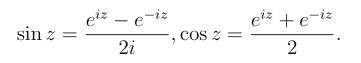
根此定义,我们不难验证复变数的正弦函数与余弦函数具有下列性质:

(1) 由于ez是以2πi为周期的周期函数,所以sin z与cos z都是以2π为周期的周期函数,即

sin(z+2π)=sin z,cos(z+2π)=cos z.

也易知sin z是奇函数,cos z是偶函数,即

sin(-z)=-sin z,cos(-z)=cos z.

(2) 由指数函数的导数公式可以求得

(sin z)′ =cos z,(cos z)′ =-sin z.

所以sin z和cos z在整个复平面上解析.

(3) 解方程sin z = 0可得z = kπ(k = 0,±1,±2,···),所以sin z的零点为z =kπ.同理可得cos z 的零点为

(4) 用定义可直接验证三角学中很多关于正弦函数和余弦函数的公式仍然成立.例如：

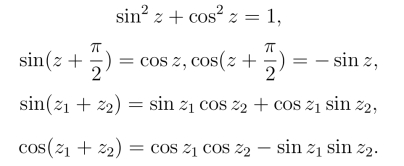
(5) 在复数域内|sin z| ≤1和|cos z| ≤1未必成立.而当|z|充分大时,|sin z|和|cos z| 都是无界的.事实上,令z =iy →∞有

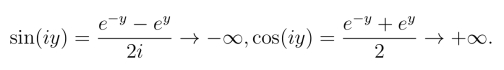
例5 求cos(1+i)的值.

解

定义5 对任意的复数z,定义

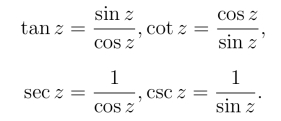
分别为z的正切、余切、正割及余割函数.它们都在分母不为零的点处解析,且有

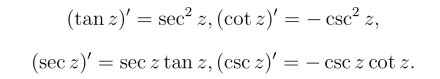
定义6 对任意的复数z,定义

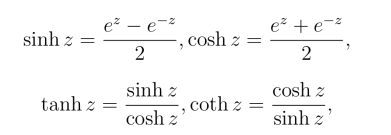
分别为z的双曲正弦、双曲余弦、双曲正切及双曲余切函数.