4.5　小结

4.5　小结

复数列αn = an+ibn(n = 1,2,···)和复数项级数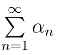的收敛定义与实数域内数列和级数的收敛定义完全类似.复数列αn = an +ibn收敛的充要条件是实数列an 和bn 同时收敛.复数项级数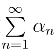收敛的充要条件是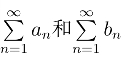同时收敛.级数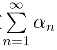收敛的必要条件是

若级数 收敛,则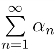必收敛,称为绝对收敛.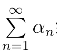绝对收敛的充要条件是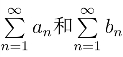同时绝对收敛.幂级数是函数项级数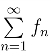中最简单的,形式为

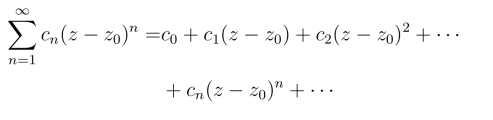
或

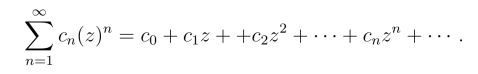
由阿贝尔定理知幂级数的收敛范围为一圆域,其圆周称为收敛圆.在圆的内部,级数绝对收敛.在圆的外部,级数发散.在圆周上要具体讨论.

收敛圆的半径称为幂级数的收敛半径.收敛半径的求法有比值法与根值法.

幂级数可以作四则运算,在收敛圆内,幂级数的和函数是解析函数,并且可以逐项求导与逐项积分.

如果函数f(z)在圆域|z-z0|＜R内解析,则在此圆域内f(z)可以展开成幂级数:

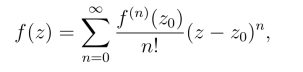
并且展开式是唯一的.

如果函数f(z)在圆环域|z-z0|＜R内处处解析,那么

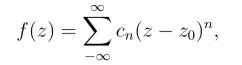(https://www.daowen.com)

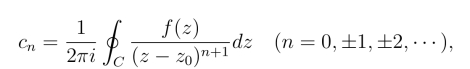
其中C为圆环域内绕z0的任何一条正向简单闭曲线,并且展开式也是惟一的.

泰勒展开式中的系数公式也可以写成

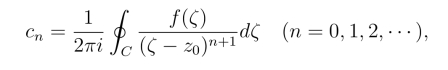
这与洛朗展开式中的系数公式

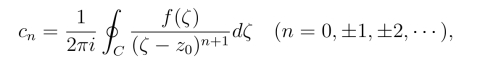
从表面上看完全一样,但是洛朗展开中的系数cn一般来说,并不等于

这是因为若z0是f(z)的奇点,那么f(n)(z0) 根本不存在,即使z0不是奇点而有f(n)(z0)存在,但在圆域|z-z0| ≤R1内可能还有其他奇点,从而简单闭曲线C内有奇点,因此Cn也不能写成但是若f(z) 在|z-z0|≤R1内处处解析,则

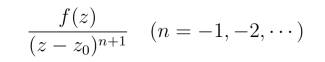
在C的内部处处解析,由柯西积分定理知

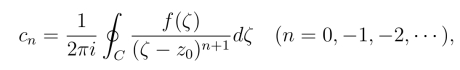
这时,洛朗级数成为泰勒级数.洛朗级数是泰勒级数的推广.

洛朗级数给我们提供了一种新的计算复积分的方法,在下一章中将进行进一步的讨论.