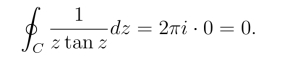5.2.3　洛必达法则

5.2.3　洛必达法则

在复变函数中,对一些未定型的极限可使用复变函数的洛必达(L’Hospital)法则.

洛必达法则设z0为函数f(z)和g(z)的零点,且在z0的某去心邻域内f(z)和g(z)都不为零,则当z →z0时,函数的极限一定存在或为无穷,且有

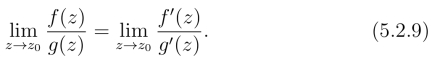
证明设z0分别为f(z)和g(z)的m,n级零点,则有

其中φ(z)与ψ(z)均在z0解析,且φ(z)0,ψ(z)0.因此

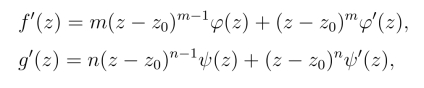
并且

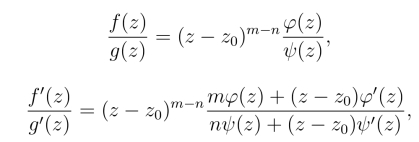(https://www.daowen.com)

从而当z →z0时,有

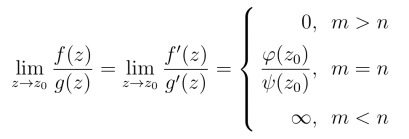
同理可证,当z0为极点时,洛必达法则也成立.

例7 计算积分C为正向圆周: |z|=1.

解 f(z)的奇点是使z tan z = 0的点.z = 0为f(z) 的二级极点,zk =kπ(k =±1,±2,···)为f(z)的一级极点.这些奇点中只有z =0 在圆周|z|=1内.

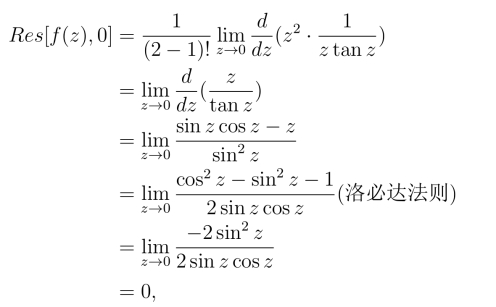
从而有