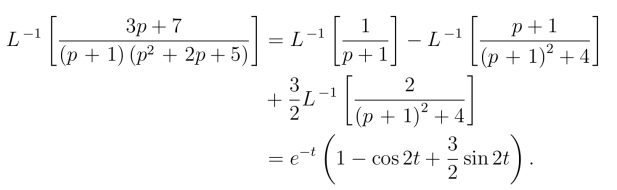8.3.2　利用留数计算反演积分

8.3.2　利用留数计算反演积分

反演积分是复变函数的积分,计算起来比较困难,但当F(p)满足一定条件时,可以用留数来计算这个反演积分.特别是当F(p)为有理函数时,计算更为简单.

定理1 设p1,p2,··· ,pn 是函数F(p) 的所有奇点,(适当选取α ＞c,使得这些奇点全在半平面Re(p)＜α内),当p →∞时,F (p)→0,则有

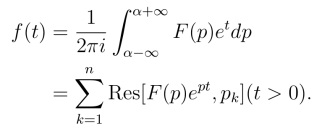
证明从略.

例1 已知F(s)= 求f(t)=L-1[F(s)].

解 (1)s1 =-1,s2 =2为F(s)的一阶极点,

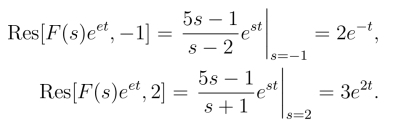
(2)

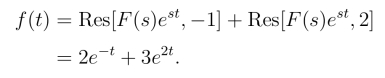
例2 求F (p)=的拉氏逆变换.

解 p1 = 0,p2 = 1分别是F (p)ep t 的一阶极点和二阶极点.由留数计算方法,

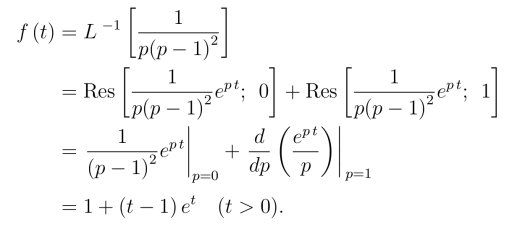(https://www.daowen.com)

求有理函数的拉氏逆变换,有时可以先把有理函数分解为部分分式,把求较复杂的函数的逆变换,化为几个较为简单的函数逆变换的和.

例3 已知F(s)= 求f(t)=L-1[F(s)]

解 (1)s1 =3,s2,3 =1±2i为F(s)的一阶极点,

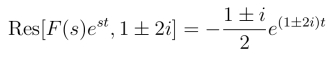
(2) f(t)=2e3t- =2e3t-et cos 2t-et sin 2t

例4 求

解 因为

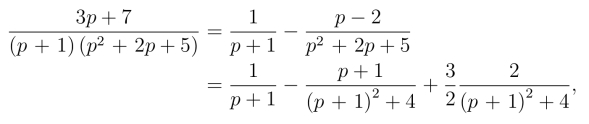
所以