5.1.3 用函数的零点判别极点的类型
若函数f(z)在点z0解析且f(z0)=0,则称z0为函数f(z)的零点.
设函数f(z)在其零点z0的邻域|z-z0|＜δ内的泰勒级数为
则c0 =0,设m是使cm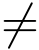 
0的最小正整数,则
定义2 若函数f(z)在z0的邻域内的泰勒级数为
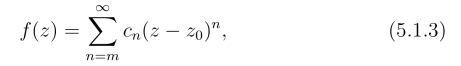
其中cm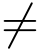 
0,m为正整数,则称z0为f(z)的m级零点.
易见,z0为f(z)的m级零点的充分必要条件为存在解析函数φ(z),且φ(z0)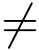
0,函数f(z) 在z0 的某邻域内能表示成
例如,z =1为f(z)=(z-1)2的2级零点.
另外,我们还可以通过f(z)在点z0的导数的值给出z0为f(z)的m级零点的充分必要条件.
定理1 z0为函数f(z)的m级零点的充分必要条件为f(z)在z0解析,f(z0)=f′(z0)=···=f(m-1)(z0)=0且f(m)(z0)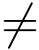
0.
证明 若z0为f(z)的m级零点,则f(z)在z0的邻域内的泰勒级数可展成式(5.1.3)的形式,对幂级数逐项求导,可得
反之,若f(z)在z0解析,f(z0)=f′(z0)=···=f(m-1)(z0)=0且f(m)(z0)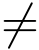
0,设f(z) 在z0 的邻域内的泰勒级数为
由系数公式知cn =
= 0(n = 0,1,2,··· ,m-1),而cm = 
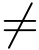0,即z0 为f(z) 的m 级零点.
下面给出用函数的零点判断极点的方法:
定理2 若函数f(z)和g(z)在点z0 解析,则有
(1) 当z0分别为f(z)和g(z)的m,n级零点时,z0为f(z)g(z) 的m+n级零点,若m ＜n,则有z0为
的n-m级极点.
(2) 当z0为g(z)的n级零点,但f(z0)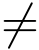
0时,z0为
的n 级极点.
证明(1)由于z0分别为f(z)和g(z)的m,n级零点,故存在函数φ(z)和ψ(z)在点z0解析,且φ(z0)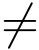
0,ψ(z0)
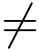0,使
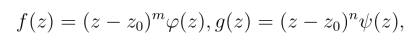(https://www.daowen.com)
从而有
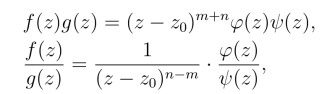
由式(5.1.4)和式(5.1.2)可知结论(1) 成立.
(2)设
则
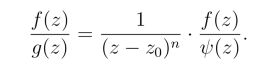
由于
在点z0解析,且
故z0为
的n级极点.
在定理2的(2)中令f(z)=1可得
推论 若z0为g(z)的n级零点,则z0为
的n 级极点,反之也成立.
例1 下列函数有些什么奇点? 如果是极点,指出它的级.
(1) f(z)=
(2) f(z)=
(3) f(z)= 
解 (1)f(z)=
的奇点是分母的零点.
由于(sin z)′ = cos z,而cos z在zk解析且cos zk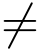 
0(k = 0,±1,±2,···),由定理2中的(2)知zk(k =0,±1,±2,···) 均为f(z)的简单极点.
(2)易见z =1,z =-1是f(z)的奇点.由于
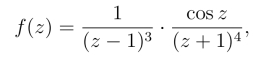
函数
在z =1解析且
因此z =1 是f(z) 的三级极点.
同理,z =-1是f(z)的四级极点.
(3)z =0是f(z)的极点,由于
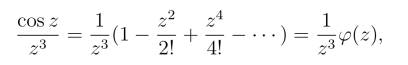
其中φ(z)在z =0解析且φ(0)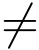
0,z =0为f(z) 的三级极点.