4.1.1　复数列的收敛性及其判别法

4.1.1　复数列的收敛性及其判别法

设α1,α2,··· ,αn,··· 为一个复数列,其通项为α=an+ibn,可简记该复数列为{αn}.

定义1 设{αn}为一个复数列且α = a+ib为复常数.若对任意正数ε都存在对应的正整数N,使当n ＞N时恒有|αn-α| ＜ε,则称该复数列收敛且其极限为α,记为

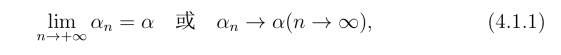
这时也称复数列{αn}收敛于α,如果不存在任何有限复常数α使得复数列{αn} 收敛于α,则称复数列{αn}是发散的.

由复数列{αn}收敛的定义可以得到下面的结论.

定理1 当n →∞时有

复数列的收敛性可以转化对两个实数列的收敛性的判定.

定理2 复数列αn收敛于α的充要条件是

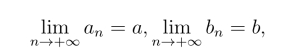
证明 若则对于任意给定的ε ＞0,都能找到一个正整数N,当n ＞N 时

从而有

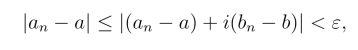
所以

(https://www.daowen.com)

同理

反之,如果 则存在一个正整数N,当n ＞N时

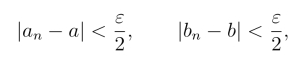
从而有

所以

例1 判别下列数列的收敛性和极限.

解 (1)令an +ibn = 则an = 0,bn =显然an →0 且bn →1/2(n →∞),于是由定理2,该数列当n →∞时收敛,其极限为i/2.

(2)显然,当n →∞时,由定理1,该数列收敛且极限为零.

(3)由于因此an =0,bn =sin((n+且当n →∞时数列bn 发散.于是由定理2得该数列发散.

定理3(柯西收敛准则) 复数列αn收敛的充分必要条件是: 对任意给定的ε ＞0,存在自然数N,使当n ＞N 时,对于任何自然数P,有

这个定理可用定理2与实数数列的柯西收敛准则来证明.