习题七
1.连续周期信号的频谱的特点是_____.
(A)周期连续频谱 (B)周期离散频谱
(C)非周期连续频谱 (D)非周期离散频谱
2.信号的频谱是周期连续谱,则该信号再时域中为_____.
(A)连续的周期信号 (B)离散的周期信号
(C)连续的非周期信号 (D)离散的非周期信号
3.下列变换不正确的是_____.
(A)F[δ(t)]=1 (B)F[u(t)]=
+πδ(w)
(C)F-1[2πδ(w)]=1 (D)F-1[cos w0t]=δ(w-w0)+δ(w+w0)
4.下列变换正确的是_____.
(A) F[δ(t)]=1 (B)F[1]=δ(w)
(C) F-1[δ(w)]=1 (D)F-1[1]=u(t)
5.某周期奇函数,其傅里叶级数中_____.
(A)不含正弦分量 (B)不含余弦分量
(C)仅有奇次谐波分量 (D)仅有偶次谐波分量
6.设F(w)=2πδ(w-w0),则F-1[F(w)]=_____.
(A)1 (B)δ(t-t0) (C)eiw0t (D)e-iw0t
7.设F(w)=F[f(t)],则F[f(1-t)]=_____.
(A)F(w)e-iw (B)F(-w)e-iw (C)F(w)eiw (D)F(-w)eiw
8.设F(w)=F[f(t)],则F[tf(2t)]=_____.
9.积分
=_____.
(A)2(t3+4)(B)8(C)-10(D)10
10.下列命题不正确的是_____.
(A)设F(w)=F[f(t)],则F[f(1-t)]=F(-w)e-iw;
(B)设F[f(t)]=F(w),若f(t)为奇函数,则F(w)为偶函数;
(C)
(D)设F[f(t)]=F(w),则2πF[f2(t)]=
11.设f(t)=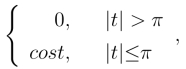
则F[f(t)]=______________.
12.设F[f(t)]=F(w),则F[f(t)cos w0t]=______________.
13.设F[f(t)]=
则f(t)=______________.
14.已知信号的频谱函数F(jw)=δ(w+π)-δ(w-π),该信号为______________.
15.F[u(t-2)]=______________.
16.F-1[δ(w-w0)]=______________.
17.F[δ(t+1)+e-it]=______________.
18.F[sin 2t cos t]=______________.
19.
=______________.
20.设a ＞0,则积分
=______________.
21.已知f(t)=e-t(t ≥0),
(1) 求f(t)的正弦傅氏积分公式；
(2) 利用(1)证明：
22.利用傅氏变换解积分方程
23.若单位冲击函数的时间间隔为T1,用符号δT(t)表示周期单位冲击序列,即
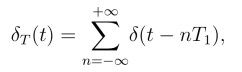
求单位冲击序列的傅里叶级数和傅里叶变换.
24.试求矩形脉冲f(t)=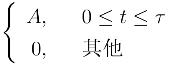
的傅氏变换.
25.求f(t)=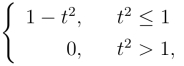
的傅氏积分,并计算
26.求符号函数sgn(t) =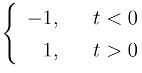
的傅氏变换.(提示sgn(t) =2u(t)-1)
27.已知f(t)的傅氏变换为F(w)=
求f(t).
28.利用位移性质求下列函数的傅氏变换：
29.求函数f(t)=
的傅氏变换.
30.设F[f(t)]=F(w),求F[tf′(t)].
31.利用象函数位移性质求下列函数的傅氏变换：
(1)求F[f(t)cos w0t];
(2)求F[f(t)sin w0t].
32.分别用象函数位移性质和卷积定理求下列函数的傅氏变换：
(1)求F[u(t)cos w0t];
(2)求F[eiw0tu(t)].
33.证明：f(t)*δ(t)=δ(t)*f(t)=f(t).
34.设F(w)=F[f(t)],证明：F[F(-t)]=2πf(w).