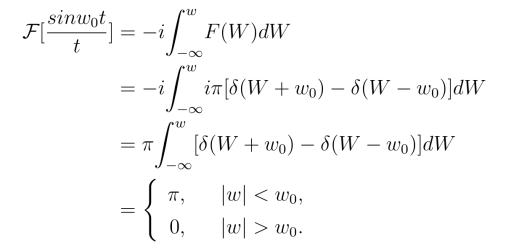7.3 傅里叶变换的基本性质
这一节,我们将介绍傅氏变换的几个重要性质,为了叙述方便,假定以下需求傅氏变换的函数都满足傅氏积分定理中的条件.
1.线性性质
设F1(w)=F[f1(t)],F2(w)=F[f2(t)],α,β是常数,则
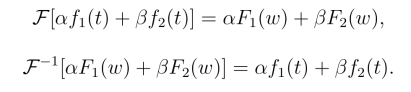
由于傅氏变换,傅氏逆变换是由积分定义的,而积分具有线性性质,所以傅氏变换,傅氏逆变换也具有线性性质.
2.位移性质
设F[F(t)]=F(w),则
![]()
这个性质也称为时移性,它表明时间函数f(t)沿t 轴向左或向右移t0的傅氏变换,等于f(t)的傅氏变换乘以因子eiwt0 或e-iwt0.
证明 由傅氏变换定义,令u=t±t0,得
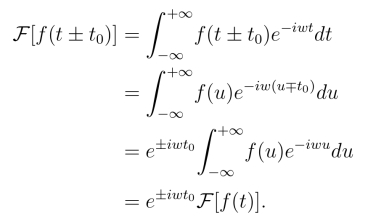
同样,傅氏逆变换有类似的位移性质,即
![]()
例1 求矩形脉冲f(t)=
解 由傅氏变换定义,
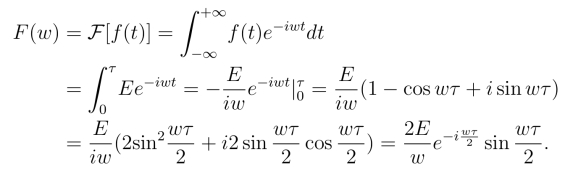
下面利用平移性质来计算.
设
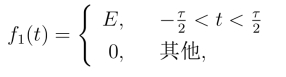
则
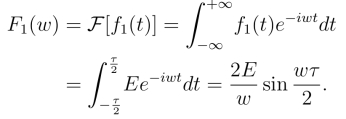
由位移性质
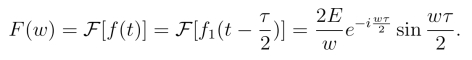
例2 设F[f(t)]=F(w),求F[f(t)cos w0t] 和F[f(t)sin w0t].
解 由傅氏逆变换平移性质,可得
![]()
因此
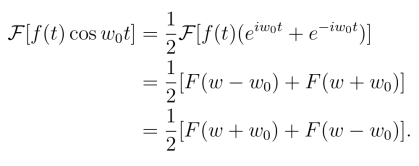
同样
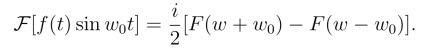
3.相似性质
设F[f(t)]=F(w),a为非零常数,则
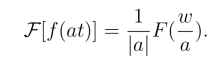
证明 设u=at,则当a >0时,
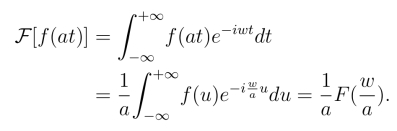
当a <0时,
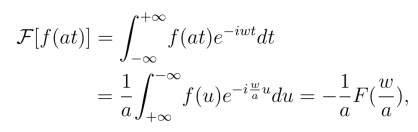
总之
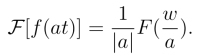
特别是当a=-1时,有如下翻转性质,
![]()
同样,傅氏逆变换也有类似的相似性质,即(https://www.daowen.com)
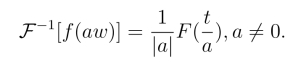
4.对称性质
设F[f(t)]=F(w),则
![]()
证明 由f(t)=![]() 得
得
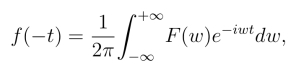
将t与w互换,有
F[F(t)]=2πf(w).
5.微分性质
如果f′(t)在(-∞,+∞)上连续或只有有限个可去间断点,且当|t|→+∞时,F[f(t)]=F(w),则
F[f′(t)]=iwF(w).
证明 由傅氏变换定义,并利用分部积分可得
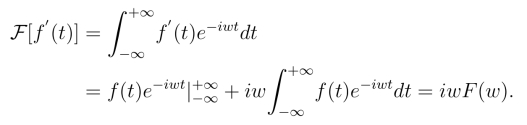
推论 如果f(n)(t)在(-∞,+∞)上连续或只有有限个可去间断点,且当|t|→+∞时,f(k)(t)→0,k =1,2,··· ,n-1,F[f(t)]=F(w),则
F[fn(t)]=(iw)nF(w).
注 为了证明简单起见,这里附加了条件|t| →+∞时,f(t) →0.事实上,满足傅氏积分定理条件的函数,其附加条件必成立,且推论中的附加条件,|t|→+∞时,fk(t)→0,k =1,2,··· ,n-1也成立.
同样,傅氏逆变换也有类似的性质,即若F-1[F(w)]=f(t),则
F-1[F′(w)]=-itf(t),F-1[F(n)(w)]=(-it)nf(t).
或换一种表示形式为
F′(w)=F[-itf(t)],Fn(w)=F[(-it)nf(t)].
6.积分性质
设F[f(t)]=F(w),如果t →+∞时,g(t)=![]() 则
则
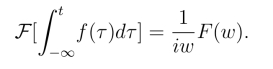
证明 因为
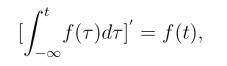
所以
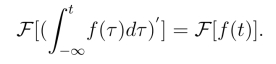
由微分性质
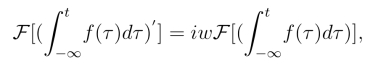
于是
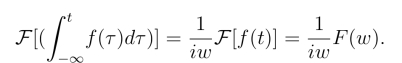
注 如果条件t →+∞时,g(t)=![]() 不成立,性质应为
不成立,性质应为
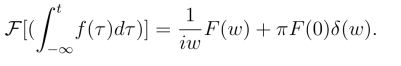
同样,傅氏逆变换也有类似的积分性质,即
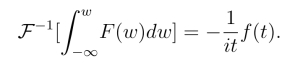
或换一种表示形式为
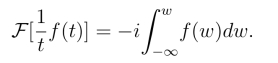
例3 求![]()
解 因为
![]()
由傅氏逆变换的积分性质,得