习题二
1.计算cos(2i)的结果为_____.
(A)sinh 2 (B)cosh 2 (C)tanh 2 (D)coth 2 2.1-i的实部为_____.
(A)ekπ(B) e-kπ(C)e2kπ(D)e-2kπ
3.设f(z)=
则f(z)的奇点的个数为_____.
(A)0 (B)1 (C) 2 (D)3
4.函数f(z)在z0处连续的充要条件是_____.
(A)可导 (B)
存在
(C)
=f(z0) (D)解析
5.下列式子中正确的是_____.
(A)ln z的定义域为z ＞0 (B)|sin z|＜1
(C)ez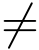
0 (D)z-3的定义域为全平面
6.设ez =i-i,则Rez =_________.
7.在复平面上,函数f(z)=
在_________不可导.
8.设f(z) = my3 +nx2y +i(x3 +lxy2)为解析函数,则m =_____,n =_____,l=_____.
9.函数f(z)=arg z在__________上不连续.
10.设f(z)=sin z,则f(2z)=_________.
11.设f(z) = u(x,y) + iv(x,y)是解析函数,若u(x,y) = y,则f′(z) =_________.
12.Ln(-3+4i)=__________.
13.
=_________.
14.函数w =z2把z平面上的直线段Rez =-1,-1 ≤Imz ≤1变成w平面上的什么曲线？
15.函数
把z平面上的下列曲线变成w平面上的什么曲线？
(1)x2+y2 =4 (2)x=1(3)y =x(4)(x-1)2+y2 =1.
16.已知函数w =z3,试求：(https://www.daowen.com)
(1)z1 =i,z2 =1+i,z3 =
+i在w平面上的象;
(2)区域0 ＜arg z ＜
在w平面上的象.
17.下列函数在何处可导？何处解析？
(1)f(z)=x2-iy;(2)f(z)=z2+2iz
(3)f(z)=
;(4)f(z)=sin x cosh y+i cos x sinh y.
18.设f(z)=
求f(z)的奇点.
19.求下列函数的导数并指明其解析区域.
(1)f(z)=sin z+3iz;(2)f(z)=
(3)f(z)=|z2|z;(4)f(z)=zImz-Rez
(5)w =|z|2-iRez2.
20.设函数f(z)在区域D内解析.试证：若它满足下列条件之一,则它在D内是常数.
(1)Ref(z)在D内为常数; (2)
在D内解析;
(3) |f(z)|在D内为常数; (4) arg f(z)在D内为常数.
21.试证明：
22.设f(z)是解析函数,试证
23.求下列复数的值：
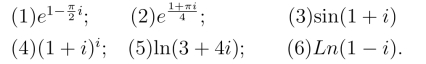
24.解下列方程.
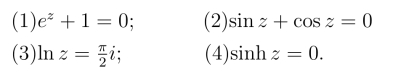
【注释】
[1]一般称为平面点集