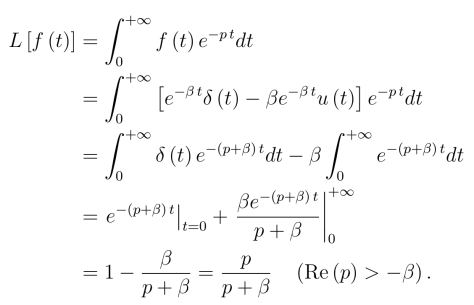8.1.4　δ-函数的拉氏变换

8.1.4　δ-函数的拉氏变换

当f(t)满足拉氏变换存在定理条件,f(t)在t=0 的邻域有界时,积分

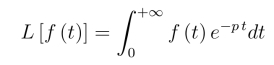
中的下限取0-或0+积分结果相同.但当f(t)在t = 0的邻域无界,特别是f(t)在t = 0 的邻域包含了脉冲函数时,拉氏变换的积分下限必须明确指出是0- 还是0+,这是因为

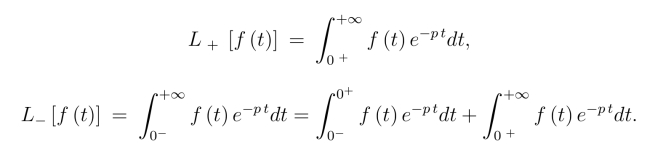
当f(t)在t=0的邻域有界时,

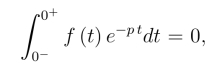
此时

但当f(t)在t=0处包含了脉冲函数时,

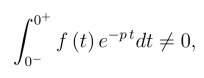
此时

(https://www.daowen.com)

为了考虑这种情况,我们需把要进行拉氏变换的函数f(t)的定义域改变为当t ＞0及在t=0的任意一个邻域内有定义.这样f(t)的拉氏变换应为

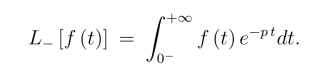
但为了书写方便,仍写为

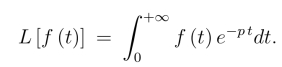
例6 求单位脉冲函数δ(t)的拉氏变换.

解 根据上面的讨论,并利用δ(t)-函数的筛选性质

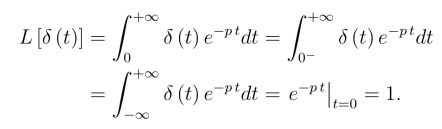
例7 求函数

的拉氏变换.

解