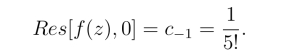5.2.1 留数的定义和计算
若z0为函数f(z)的孤立奇点,则f(z)在z0的某个去心邻域0 <|z-z0|<R内解析.由解析函数积分的闭路变形原理,对于该邻域内任意一条围绕点z0的正向简单闭曲线C,f(z) 沿C的积分取定值,下面利用该积分来定义留数.
定义1 设z0(z0 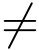 ∞)为函数f(z)的孤立奇点,C为0 <|z-z0|<R内围绕z0的任一条正向简单闭曲线,称积分
∞)为函数f(z)的孤立奇点,C为0 <|z-z0|<R内围绕z0的任一条正向简单闭曲线,称积分
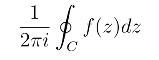
为f(z)在点z0处的留数(Residue),记作Res[f(z),z0].
设函数f(z)在z0的去心邻域0 <|z-z0|<R的洛朗级数为式(5.1.1),由洛朗级数的系数公式有
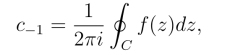
从而有
![]()
即f(z)在z0的留数就是f(z)在以z0为中心的圆环域内的洛朗级数中(z-z0)-1的系数.
一般情况下,用定义1来计算留数很困难,对于z0 为f(z)的可去奇点,极点或本性奇点的情形,其留数都可用式(5.2.1) 来计算,故称它为计算留数的一般公式.例如,由该式可直接推出: 若z0为f(z)的可去奇点,则它在点z0 的留数为零.
又如,当z0为f(z) = g(z-z0)的孤立奇点时,若以g(ζ)为偶函数,则f(z)在点z0的去心邻域内的洛朗级数只含ζ = z-z0的偶次幂,其奇次幂系数都为零.于是令ζ =z-z0得
![]()
由式(5.2.2)可以看出,函数
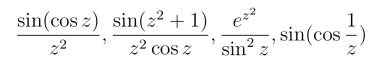
等,在奇点z = 0处的留数都为零.将这些函数的变量z换为z-z0,z0为这些新函数的孤立奇点,它们在点z0的留数也都是零.
为求函数在其孤立奇点的留数,我们只要求出它在z0的去心邻域内的洛朗级数,从而得到(z-z0)-1的系数c-1,即函数在点z0的留数.但对于有的类型的奇点,这样做是繁琐的并且也没有必要.
对于z0为极点的许多情形,用下列规则更简便
规则1° 若z0为f(z)的1级极点,则有
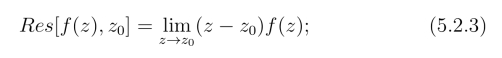
规则2° 若z0为f(z)的m级极点,则对任意整数n ≥m有
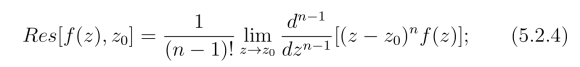
规则3° 设f(z) = ![]() 其中P(z)和Q(z)在点z0 都解析.若P(z0)
其中P(z)和Q(z)在点z0 都解析.若P(z0) 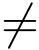 0,Q(z0)=0 且Q′(z0)
0,Q(z0)=0 且Q′(z0)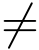 0则z0 为f(z) 的1级极点,且有
0则z0 为f(z) 的1级极点,且有
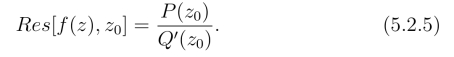
说明 将函数的零阶导数看作它本身,规则1°可看作规则2° 当n=m=1时的特殊情形,且规则2° 可取m=1.
证明 先证规则2°,由于z0 为f(z)的m级极点,因此可设在0 <|z-z0|<R内有
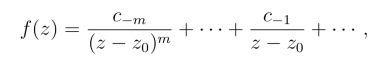
以(z-z0)n乘上式两端,得
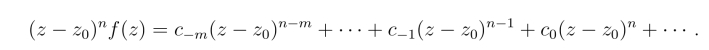
由于洛朗级数在其收敛的圆环域内可以逐项求导,上式两边求n-1阶导数,由于n ≥m,则有
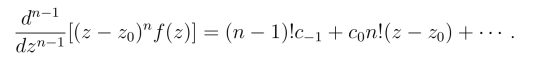
令z →z0取极限,得(https://www.daowen.com)
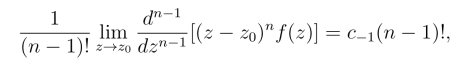
两端再除以(n-1)!即得规则2°.
上面证明中,取n=m=1就是规则1°的证明,下面只需证明规则3°.
由于Q(z0) = 0及Q′(z0) 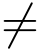 0,因此z0 为Q(z)的1级零点,又因P(z0)
0,因此z0 为Q(z)的1级零点,又因P(z0) 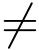 0,故z0为f(z)=
0,故z0为f(z)= ![]() 的1级极点.于是由上述规则1° 得在使用规则2°时,一般取n = m,这是因为n取得越大,求导的次数越多,使得计算很复杂.
的1级极点.于是由上述规则1° 得在使用规则2°时,一般取n = m,这是因为n取得越大,求导的次数越多,使得计算很复杂.
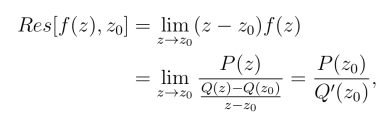
例1 求下列函数在指定点处的留数.
(1) f1(z)=![]() ,z =0及z =1;
,z =0及z =1;
(2) f2(z)= ![]() ,zk =kπ(k =0,±1,±2,···).
,zk =kπ(k =0,±1,±2,···).
解 (1)z =0是f1(z)的简单极点,由规则1°,得
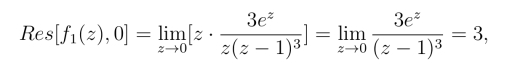
z =1是f1(z)的2级极点,由规则2°,得
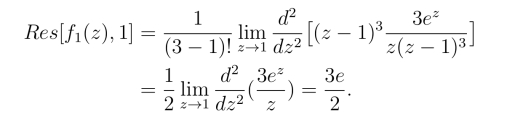
(2)zk = kπ(k = 0,±1,±2,···)是sin z 的1级零点,而cos zk 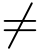 0(k =0,±1,±2,···),由规则3°,得
0(k =0,±1,±2,···),由规则3°,得
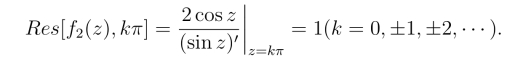
若z0是f(z)的本性奇点,一般用把f(x)展开成洛朗级数的方法计算留数.
例2 求函数f(z)=![]() 在z =0的留数.
在z =0的留数.
解 z =0是f(z)的本性奇点,在圆环域0 <|z|<∞的洛朗级数为
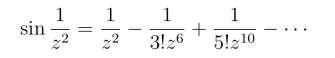
得c-1 =1,因此Res[f(z),0]=1.
若极点的级较高(3级以上),我们也往往用把函数展开成洛朗级数的方式求留数.
例3 求函数f(z)= ![]() 在z =0的留数.
在z =0的留数.
解 z = 0是函数ez -1的1级零点,又是函数z6 的六级零点.于是它是f(z)的5级极点,即m=5,可用规则2°计算其留数.
若取n=m=5,则
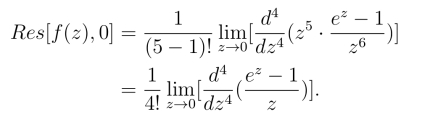
导数的计算比较复杂.为了计算简便应当取n=6,这时有
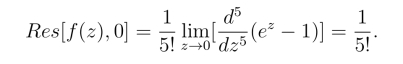
另外,f(z)在点z0 =0的去心邻域0 <|z|<∞内的洛朗级数为
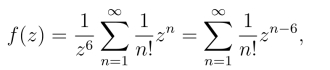
其中n=5的项的系数为![]() 从而也有
从而也有