习题三
1.计算f(z)=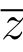 /(|z|)沿下列曲线的积分.
/(|z|)沿下列曲线的积分.
(1) C1为正向圆周|z|=2;(2) C2 为正向圆周|z|=4.
2.计算f(z)=|z|沿下列曲线的积分.
(1) C1为从点z1 =-1到z2 =1的直线段;
(2) C2为从点z1 =-1到z2 =1的上半圆周;
(3) C1为从点z1 =-1到z2 =1的下半圆周.
3.设C为从点z = 0到z1 = 1 + i的抛物线y = x2,计算函数f(z) =x2+iy沿C的积分.
4.设C为从点z = 0到z1 = 1 +i的直线段,计算函数f(z) = x - y +ix2沿C的积分.
5.利用复积分的估值性质5°证明下面不等式.
(1)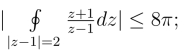
(2)![]() ≤2,C是从z1 =i到z2 =2+i的直线段;
≤2,C是从z1 =i到z2 =2+i的直线段;
(3)![]()
6.设f(z)在正向圆周|z-z0|=ρ上连续,且在该圆周C上处处有|f(z)|≤M(ρ >0),还设
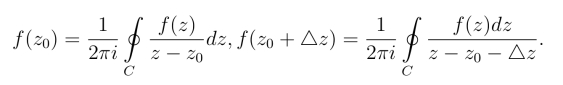
试用复积分的估值性质证明当|△z|≤ρ/2时有
(1)![]()
(2)令△z →0可得
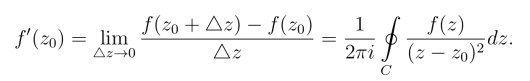
7.若函数f(z)在简单闭路C上解析,在C的内部只有奇点z0,则它沿C的积分不为零,对吗?为什么?
8.试说明下列积分值一定为零,为什么?
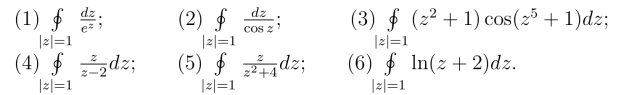
9.试讨论函数f(z) =![]() 沿正向圆周|z -z0| = r的积分值,其中r >0,且|z0|
沿正向圆周|z -z0| = r的积分值,其中r >0,且|z0|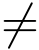 r,|z0|
r,|z0|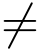 0.
0.
10.设C和C1分别为正向圆周|z| = 2和|z| = 1,且Γ = C + C-1 ,则有![]() 为什么?
为什么?
11.计算下列积分值,其中积分路径都取正向.

12.用柯西积分定理计算积分I =![]() 的值,且证明等式
的值,且证明等式
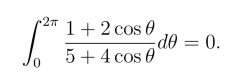 (https://www.daowen.com)
(https://www.daowen.com)
13.求积分![]() 的值.
的值.
14.计算下列积分,且说明其积分路径的允许范围.
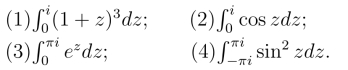
15.计算积分![]() 其中C为从点z1 =-i 到点z =i的右半圆周.
其中C为从点z1 =-i 到点z =i的右半圆周.
16.计算积分![]() 其中
其中![]()
17.计算下列积分,其中积分闭路取正向.
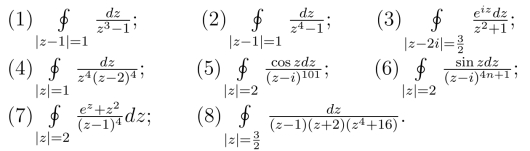
18.设C1和C2时互不相交且互不包括的正向简单闭路,且z0是不在曲线C1和C2上的一定点,试讨论下面积分I 的值
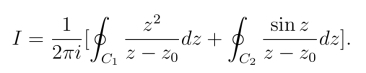
19.设z0为复常数且|z0| 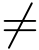 1,f(z) = ez/(z -z0)3,试讨论f(z)沿正向圆周|z0|=1 的积分值.
1,f(z) = ez/(z -z0)3,试讨论f(z)沿正向圆周|z0|=1 的积分值.
20.用柯西积分公式计算函数f(z) = ez/z沿正向圆周|z| = 1的积分值.然后利用圆周|z|=1 的参数方程z =eiθ(-π ≤θ <π)证明下面积分
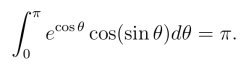
21.设f(z)和g(z)在简单闭路C上及其内部解析,试证:
(1)若f(z)在C上及其内部解析,则有
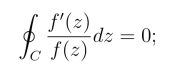
(2)若在C上有f(z)=g(z),则在C的内部有f(z)=g(z).
22.设函数f(z)在单连通域D内连续,且对于D内任何一条简单闭曲线C都有![]() 证明f(z) 在D 内解析(Morera 定理).
证明f(z) 在D 内解析(Morera 定理).
23.设u=u(x,y)为区域D内的调和函数,试证函数f(z)=ux-iuy在D内解析.
24.设u=u(x,y)和v =v(x,y)都是区域D内的调和函数,试证函数f(z)=(uy-vx)+i(ux+vy) 在D内解析.
25.由下面所给调和函数求解析函数f(z)=u+iv.
(1)u(x,y)=x3-3xy2,f(0)=i;
(2)v =2xy,f(i)=-1;
(3)u=ex(x cos y-y sin y),f(0)=0;
(4)u=(x-y)(x2+4xy+y2),f(0)=0;
(5)v =y/(x2+y2),f(2)=0.
26.若v是u的共轭调和函数,试问u是否也一定是v的共轭调和函数?为什么?
27.设f(z) = u(x,y) + iv(x,y)在区域D内解析且处处不等于零,试证g(x,y)=ln|f(z)| 在D 内为调和函数.
