7.2.3 广义傅氏变换
2026年01月14日
7.2.3 广义傅氏变换
傅里叶变换是一个强大的数学工具,但是在物理和工程问题中,有许多函数不满足绝对可积条件,即不满足条件:
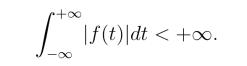
例如常数函数,正弦函数等.利用傅里叶变换的定义及δ-函数的结果,也可以求出这类函数的傅里叶变换.但是不同于上小结所讲的傅里叶变换,这里是广义傅里叶变换,但一般也将广义傅里叶变换直接称为傅里叶变换.
由傅氏变换的定义和δ-函数的筛选性质,
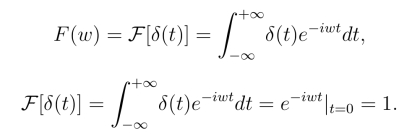
由于傅氏变换与傅氏逆变换是一个变换对,所以得到1的傅氏逆变换为
![]()
一般有
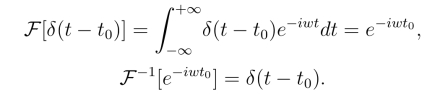
因为
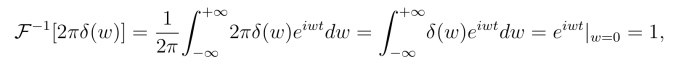
所以
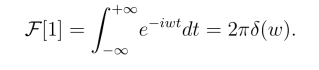 (https://www.daowen.com)
(https://www.daowen.com)
同样因为
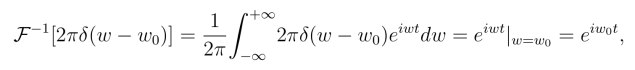
所以
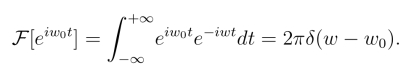
这样我们得到了四个有用的傅氏变换对:
![]()
由于δ(t),1,eiw0t等都不是(-∞,+∞)上绝对可积函数,按照常义它们与e-iwt乘积在(-∞,+∞) 不收敛,所以它们的傅氏变换都是广义的.以下几个例子中函数的傅氏变换也都是广义傅氏变换.为了叙述简单,以后广义傅氏变换也称为傅氏变换.
例4 求正弦函数f(t)=sin w0t的傅里叶变换.
解
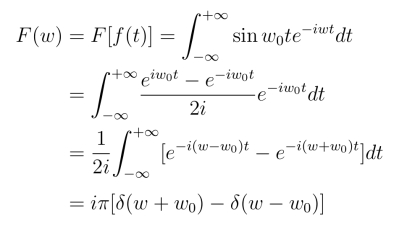
类似地,
![]()
