8.6　小结

(1)在高等数学中经典的解常系数线性微分方程的步骤是：先求齐次方程相应的特征方程的根,得出齐次方程的线性无关的特解,由此得到齐次方程的通解; 再求非齐次方程的一个特解,从而得到非齐次方程的通解；利用给定的初始条件,解出该初值问题的解.如果用拉氏变换解同样问题,方程(无论是齐次的,还是非齐次的)两边取拉式变换时是连带初始条件的,无需先求通解再求特解,“一步到位”,显然比经典的解法便捷多了.如果初值问题的初始条件全为零,象函数的代数方程形式更为简单,解起来更为方便.当方程中非齐次项因具有跳跃点而不可微时,用经典的方法求解很困难,而用拉氏变换求解却不会因此带来任何困难(如本章习题中的第31.(5)题).再看用拉氏变换解线性微分方程组,也比高等数学中经典的方法简单多了.特别是用拉氏变换可以单独求出方程组中每一个未知函数,而不必知道其余未知函数,一般说来经典的方法是做不到的.

(2)在本章第一节中提到由于拉氏变换不涉及f(t)当t ＜0情况,故以后约定t ＜0 时,f(t) = 0,即把f(t) 理解为f(t)u(t).按此约定,在多数情况下把f(t)u(t)写作f(t) 对求它的拉氏变换不会有什么影响,但是要利用拉氏变换延迟性质时,应该留意把f(t) 看作f(t)u(t)是有条件的,即t ＜0 时,f(t)=0.延迟时间t0得到的f(t-t0),它是从t=t0 开始才有非零数值,即延迟了一个时间t0.我们可通过下面的例子更好地理解如何正确使用拉氏变换延迟性质.

例1 设f(t)=(t-2)2,求f(t)的拉氏变换.

解 下面我们用两种方法来解,看看会有什么结果.

方法一：把f(t)=(t-2)2 看作g(t)=t2 的延迟.由于利用延迟性质,得到

方法二：

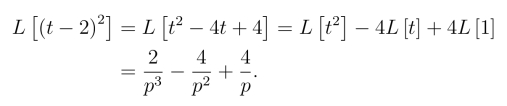
两种解法结果不同,哪种解法错了呢？第一种解法是错的.按拉氏变换的约定f(t) = (t-2)2,当t＜0时,为零,0＜t＜2时不为零.但g(t) =t2 的延迟应为g(t-2) = (t-2)2u(t-2),它在1＜t＜2 等于零.(t-2)2与(t-2)2u(t-2) 不是一回事.读者还可以通过本章习题中23题进一步体会拉氏变换延迟性质.